做过数据采集或者模拟电路的同学很可能知道下面这个关于ADC信噪比的著名公式:! |$ f2 W7 c4 h0 s$ p7 O
0wh2hf2ibhx6403028219.png
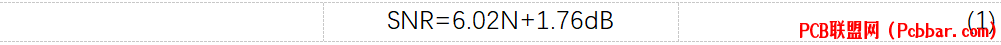 ! ?' Z$ R" o5 D3 b
! ?' Z$ R" o5 D3 b
其中N是ADC的位数,比如对于一个10bit的ADC,N=10,当ADC采集一个满量程的正弦波时,那么信噪比SNR=6.02*10+1.76=61.96dB,那么这个公式是怎么来的呢?& L2 J i+ w# ~
ADC量化噪声
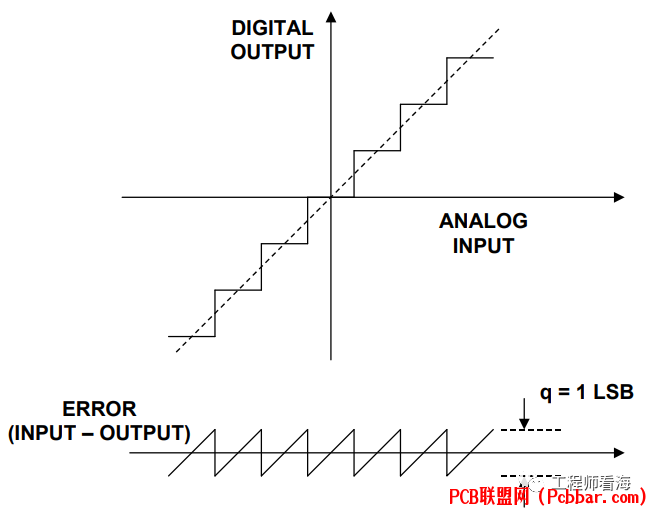
8 ^1 s+ M( B/ H& X5 N( x下图是理想ADC的量化噪声示意图,从下图可以看到,对于一个线性输入的模拟信号,ADC会产生台阶式的输出,这个输入和输出的误差波形近似于一个峰峰值q=1LSB的锯齿波,它的有效值RMS计算过程见公式(2)(q=1LSB),LSB计算过程见公式(3),其中FS是ADC的输入电压范围,。
2 J: v5 e, T# b5 _" \
wecvxg2fnb36403028319.png

' b) D$ d) n h! f: ]3 u+ c5 ~+ h0 _( L- l
baz0jag4vxx6403028419.png
: x+ D# ?% _7 `+ A6 XSNR# C8 ~$ h9 t7 W
以前的文章介绍过SNR计算过程,信噪比是信号的有效值(RMS)除以噪声的有效值(RMS),+ P' Q/ T" b* L( m5 s4 W) k
qpxybg50t0m6403028519.png
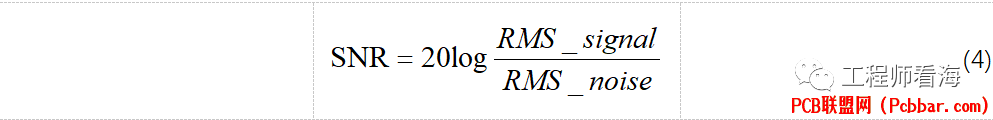 * l. k6 ~" B7 _3 f+ ~
* l. k6 ~" B7 _3 f+ ~
; R1 o# }3 B& L: x2 E
对于一个满量程输入的正弦信号见公式(5),根据公式(5)可以求得公式(6),
2 ^+ d; k/ D) l
rd2sjuaqkil6403028619.png
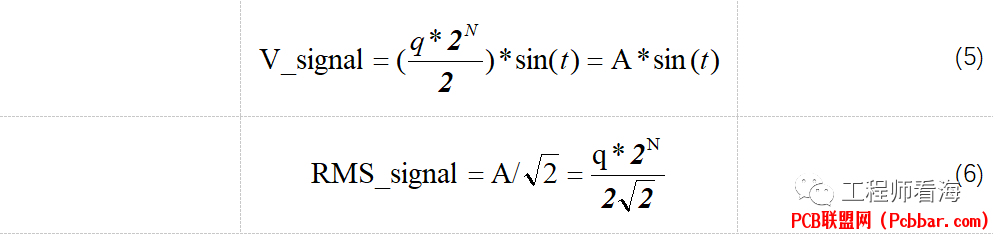
1 N' y' o5 v0 ]5 E J6 T对于满量程ADC而言,其输入范围是0-FS,那么输入的正弦信号的幅度范围就是0-Fs/2,见下图示意图,因此公式(5)中的分母是2
, I8 ^6 y- e$ \: }! f! W5 j1 \
ljuupeerysq6403028719.png
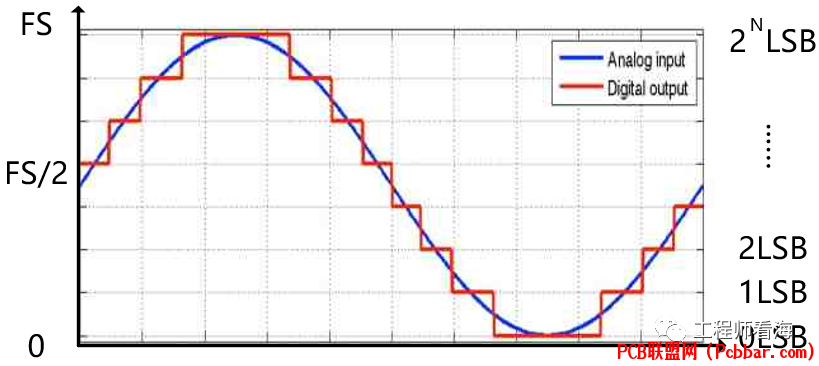
9 q6 n" V3 h( u& sADC信噪比SNR与位数N8 A8 v2 ?, c* o( C" F
那么到目前为止,我们知道了信号的有效值(RMS),即公式(6),也知道了ADC量化噪声的有效值(RMS),即公式(2)。把公式(6)和公式(2)带入公式(4)得到公式(7):
( o! p* e0 V- l3 j5 D, q _. V9 j3 Y- m
bamau0rkb3y6403028819.png
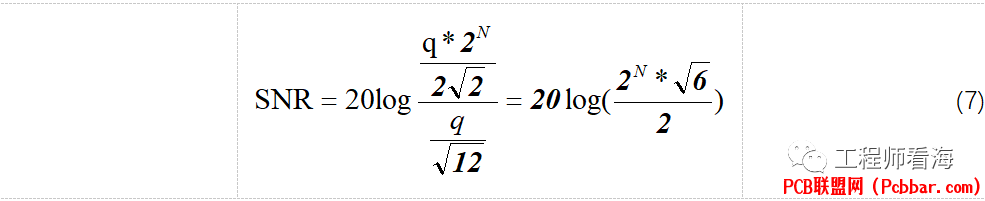 5 T% l% U) J; x& g9 o! s. b6 W' D
5 T% l% U) J; x& g9 o! s. b6 W' D
公式(7)不够简化,我们继续化简(高中学的指数运算规则),可以得到公式(8),
8 |) {8 L5 Y5 `' r5 J& n" E
nms5d3kblnb6403028919.png
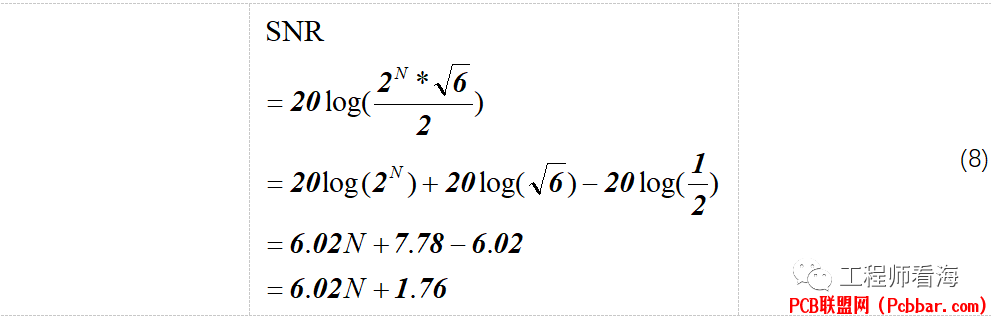 % G9 W$ P# t7 w3 v) P$ F
% G9 W$ P# t7 w3 v) P$ F
由此我们就推导出了ADC位数N与信噪比SNR的关系,是不是和公式(1)一模一样?/ J9 n; X W; W9 [1 d6 |
多说几句
$ l( W8 |4 l: a% O9 F2 y4 w! }上式的成立条件是信号带宽比较高。
: T) Z4 q1 @8 x1 @! H. n! |如果信号带宽(或者说频率)很低,低于奈奎斯特采样频率fs/2,那么这会导致信号带宽范围内的噪声减小,进而使得SNR增加。
- r3 l5 t* F8 z* o这就是常说的过采样,详细内容后面后机会在介绍。 v6 B/ g' C: }- w3 Y+ L3 i
另一点值得说明的是,在评估噪声时,常用到频谱分析,频谱的本底噪声值与采样点数量有关。0 ]; _ i( `% H& U% n9 l
如果采样点多,那么本底噪声就会低,如果采样点数量减小,那么本底噪声就会增加,这被称为FFT增益。9 }% p6 j3 [3 y! U+ I! {" @
因此在噪声分析时,最好要自始至终使用相同数量的采样点进行分析,避免被不正确的评估方法误导。 |