|
|
点击上方蓝字和“好玩的MATLAB”一起快乐玩耍吧!
9 M$ o: `) ?4 J7 Y, R0 _2 `$ W" X; V/ x
hlwyoo0casp6405195743.jpg
 ) @% O$ f9 D7 `' b# [- A" z. ]& ]
) @% O$ f9 D7 `' b# [- A" z. ]& ]
好玩的matlab
" U7 g5 e, u t& ]带你解锁不一样的matlab新玩法
! k) k( U4 H* S8 y* M
h6 T: T2 U2 D+ v今天介绍一下怎么绘制回归曲线的置信区间+边际图+核密度填充图,喜欢此推文的小伙伴们记得点赞+关注+分享!【尊重作者劳动成果,转载请注明推文链接和公众号名】4 d* {6 B. d& e$ K0 K$ m& B
: Z- b% z7 x: K, O- S; n
gsx1pbogkjd6405195843.png
 % M- ]4 H6 l1 N6 e. Y/ X2 O' M
% M- ]4 H6 l1 N6 e. Y/ X2 O' M
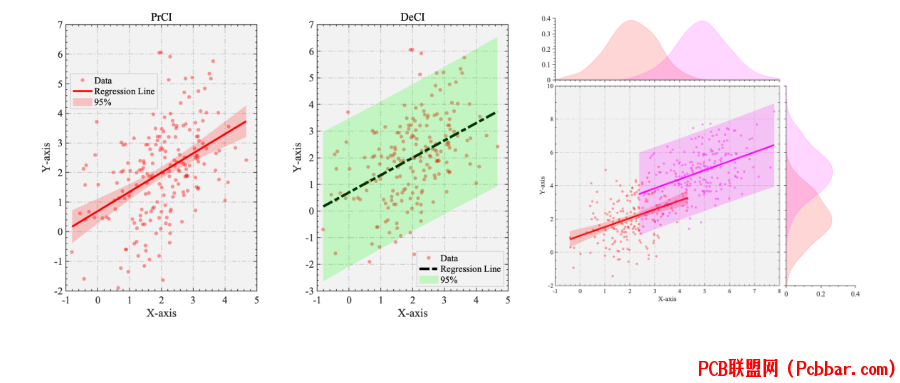
效果图
0 Y+ `3 ^5 d d) ?4 ?5 m
ky504fzhfnt6405195943.gif
0 Z( X! V; C0 w9 T! m6 e- W/ Z# F, m4 x9 M: q
cyjoektza4a6405196043.png
 " u) ?, Q" W; G5 [
" u) ?, Q" W; G5 [
6 L. |' k4 d9 y6 f* h' ?
! U' U0 B* V( D$ g& }回归线置信区间画法
6 s3 D4 r! _; y" s, q
7 { \0 P3 b' Z& o" a介绍一下绘制回归线置信区间的两种方式 p3 k/ R, n2 i1 O& s; C3 |$ L
一种方法是:
, ^1 T. i P- Rclc;clear;close all;%--------------------------------------------------------------------------% @Author: 好玩的Matlab% @公众号:好玩的Matlab% @Created: 09,06,2023% @Email:2377389590@qq.com% 尊重劳动成果,转载请备注推文链接和公众号名。% @Disclaimer: This code is provided as-is without any warranty.%--------------------------------------------------------------------------% 使用提供的数据data = repmat([2 2], 200, 1) + randn(200, 2) * [1 .5; 0 1.32];xData = data(:, 1);yData = data(:, 2);% 绘制散点图figure('Position',[383 355 886 507]);scatter(xData, yData, 'r', 'filled', 'MarkerEdgeColor', 'none', 'MarkerFaceAlpha', 0.4);hold on;% 进行线性回归linearModel = fitlm(xData, yData);% 计算回归曲线和置信区间xFit = linspace(min(xData), max(xData), 200)';[yPred, yConfInterval] = predict(linearModel, xFit, 'Alpha', 0.05); % 95%置信区间% 绘制回归曲线plot(xFit, yPred, 'r', 'LineWidth', 2);% 使用fill函数绘制置信区间fill([xFit; flipud(xFit)], [yConfInterval(:, 1); flipud(yConfInterval(:, 2))], 'g', 'FaceAlpha', 0.3, 'EdgeColor', 'none');defaultAxeslegend(gca, 'Data', 'Regression Line','95%','Confidence Interval','box','on','Location','best','EdgeColor', [1 1 1]*0.8);?2 r4 k" U+ P" Z5 Y) @. v, b# k
di0qipppk106405196144.png
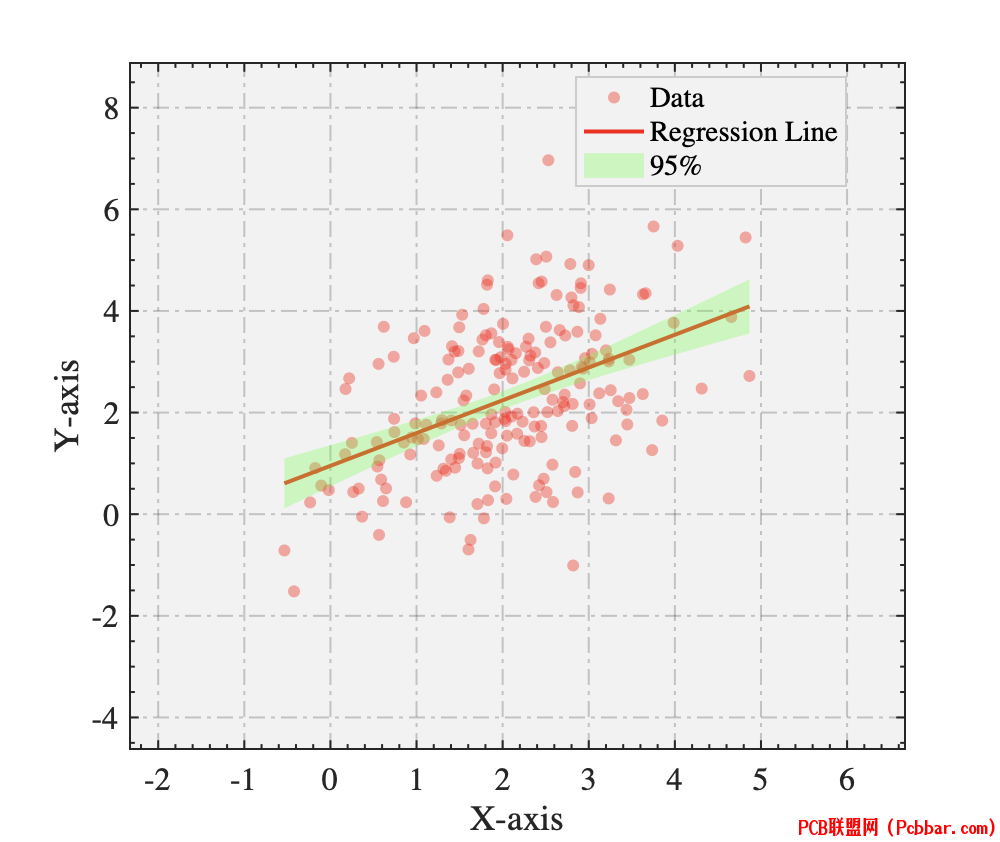
6 z5 `& y# q2 b% c8 M另一种方法是:
7 {5 M2 B( q1 Vclc;clear;close all;%--------------------------------------------------------------------------% @Author: 好玩的Matlab% @公众号:好玩的Matlab% @Created: 09,06,2023% @Email:2377389590@qq.com% 尊重劳动成果,转载请备注推文链接和公众号名。% @Disclaimer: This code is provided as-is without any warranty.%--------------------------------------------------------------------------% 使用提供的数据data = repmat([2 2], 200, 1) + randn(200, 2) * [1 .5; 0 1.32];xData = data(:, 1);yData = data(:, 2);% 创建图形窗口并持有当前图figure('Position',[383 355 886 507]);hold on;% 使用polyfit进行线性拟合[polyCoeff, polyStruct] = polyfit(xData, yData, 1);xFit = linspace(min(xData), max(xData), 200);[yFit, fitDelta] = polyval(polyCoeff, xFit, polyStruct);alpha = 0.05; % 对于95%置信区间zValue = norminv(1 - alpha/2, 0, 1); % 这将返回1.960% 计算置信区间upperConfInt = yFit + zValue .* fitDelta;lowerConfInt = yFit - zValue .* fitDelta;% 绘制原始数据scatter(xData, yData, 'r', 'filled', 'MarkerEdgeColor', 'none', 'MarkerFaceAlpha', 0.4);% 绘制拟合曲线plot(xFit, yFit, 'r', 'LineWidth', 2.5);% 使用fill函数绘制置信区间fill([xFit, fliplr(xFit)], [upperConfInt, fliplr(lowerConfInt)], 'g', 'EdgeColor', 'none', 'FaceAlpha', 0.15);defaultAxeslegend(gca, 'Data', 'Regression Line','95%','Confidence Interval','box','on','Location','best','EdgeColor', [1 1 1]*0.8);5 V. G, o+ ?6 e! o7 A5 t# g
3oqyqnkzxhx6405196244.png
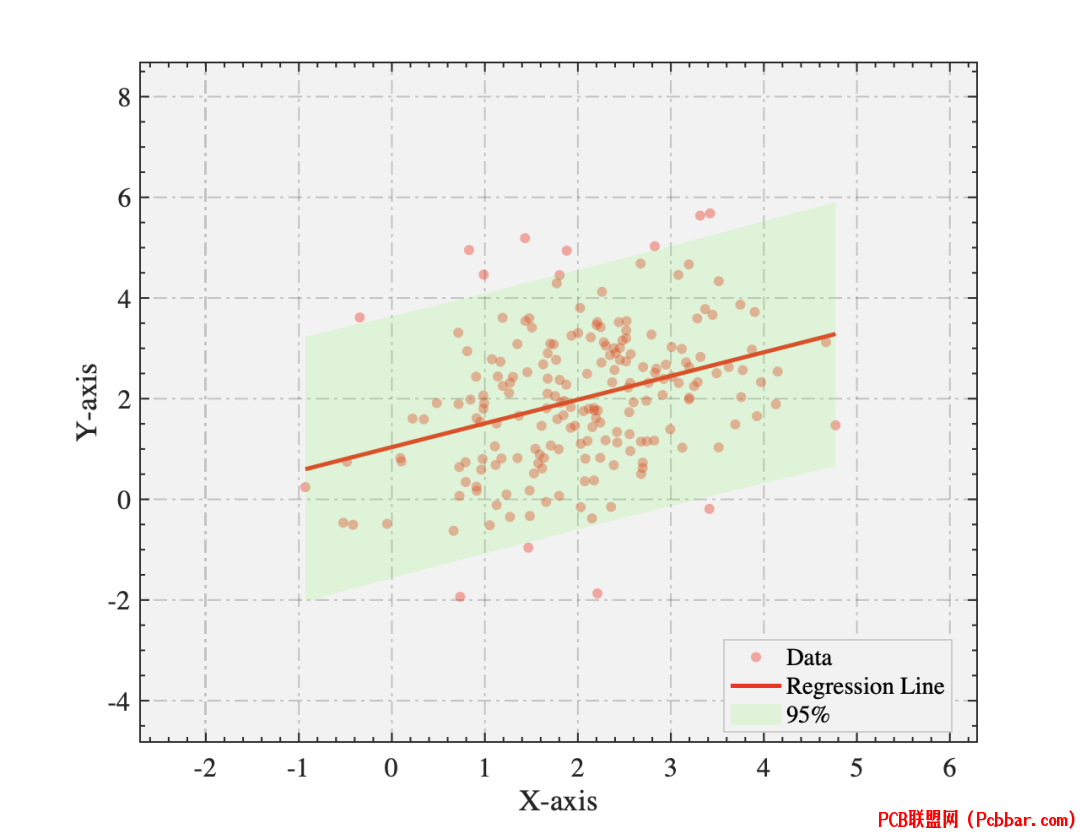
2 L6 }" a- Y! F5 J其中defaultAxes是坐标轴的设置函数如下:
) h) _: B* p1 _3 M5 f7 }$ t$ t- Vfunction defaultAxesax=gca;ax.Box='on';ax.Color = [1,1,1]*0.95;
8 s6 i" @1 _( |9 O8 A% ax.XLim=[-2,15];% ax.YLim=[-4,13];ax.XLabel.String='X-axis';ax.YLabel.String='Y-axis';ax.Title.String='';% legend(ax, 'Data', 'Regression Line', [num2str(z*100),'%'],'Confidence Interval','box','on','Location','best','EdgeColor', [1 1 1]*0.8);ax.FontName='Times New Roman';! L& s, z3 S0 R/ N1 N* a
ax.XGrid = 'on'; % 关闭X轴网格线ax.YGrid = 'on'; % 打开Y轴网格线ax.GridLineStyle = '-.'; % 设置网格线样式为虚线ax.GridColor = 'k'; % 设置网格线颜色为红色ax.GridAlpha = 0.2; % 主要网格线透明度
2 u+ h; r/ B2 A5 V' bax.XMinorGrid = 'off'; % 打开x轴次要网格线ax.YMinorGrid = 'off'; % 打开y轴次要网格线ax.MinorGridLineStyle = '-'; % 设置次要网格线样式ax.MinorGridColor = [0 0 0]; % 设置次要网格线颜色ax.MinorGridAlpha = 0.1; % 设置次要网格线透明度5 u8 f2 u3 z$ I: y' Q9 V, m
ax.LineWidth = 1; % 设置坐标轴线宽ax.XMinorTick = 'on'; % 打开x轴次要刻度线ax.YMinorTick = 'on'; % 打开y轴次要刻度线ax.TickDir = 'in'; % 设置刻度线方向向外ax.FontSize = 16; % 设置坐标轴字体大小
2 u9 q0 N9 S1 s6 Yend( n9 t. x& {! O; O/ d" c8 H2 U1 O
* t7 x1 U3 A4 x- r* W' y
% p3 k: L; O: p! s
原理介绍
& K$ k7 P) d) z简单介绍一下这两种方式的不同:
$ U7 ~. `7 @. M- c: T) Z1 h) c第一组代码使用了 fitlm 和 predict 函数,这是基于更复杂的线性模型拟合。这种方法计算了95%的置信区间,这个区间给出了模型预测响应值的不确定性。第二组代码使用了polyfit和 polyval 函数,用于多项式拟合。这里用的是多项式的一阶(线性)拟合。polyval 返回了拟合值和预测的标准误差,并假设这个标准误差是正态分布的。然后,它使用这个标准误差来计算了一个简化的95%置信区间(yFit + zValue* fitDelta)。其中:在正态分布中,以下是关于置信区间和标准偏差距离均值的规律:大约 68% 的数据点位于距离均值 1 个标准偏差以内的区间。大约 95% 的数据点位于距离均值 2 个标准偏差以内的区间。大约 99.7% 的数据点位于距离均值 3 个标准偏差以内的区间。这些规则是基于正态分布的数学属性,特别是在描述数据集分布的集中趋势和离散程度方面。这些比例也常被称为 "68-95-99.7" 规则或者 "三西格玛(Three-Sigma Rule)"或者“拉依达(Laplace)” 规则。很容易得出要想得到95%的置信区间,则: ;
/ Q* C9 {( a4 I# q要得到任意的置信区间则用以下代码计算:9 y0 ?( D {5 u" G2 R- T5 P$ y
alpha = 0.05; % 对于95%置信区间zValue = norminv(1 - alpha/2, 0, 1); % 这将返回1.960% 计算置信区间upperConfInt = yFit + zValue .* fitDelta;lowerConfInt = yFit - zValue .* fitDelta;由于这两种方法背后的统计模型和假设不同,所以得到的置信区间也可能会不同。具体使用哪一种方法取决于你的数据特性和需求。如果你的数据更适合一个复杂的线性模型,并且你希望考虑更多的变量和相互作用,fitlm 可能会更适合。如果你的数据是简单的并且你只是需要一个快速和简单的拟合,polyfit 和 polyval 可能就足够了。fitlm 方法更全面,计算的置信区间通常更为准确,特别是当数据复杂或存在不确定性时。
- s% g8 l& }) w, t+ B. }& xpolyfit 方法则更简单和快速,但可能不如 fitlm 那样准确。
+ p$ p/ ~3 o/ F$ C& F& j6 a9 f总结:两个不同的置信区间,是因为这两种方法用不同的方式来估计这个区间。根据你的具体需求和数据的性质,选择其中一种方法。" P5 K2 R' u/ ~) c0 I2 C/ C( |3 H
0 R' h1 Y3 w" Z, `! M# a+ n8 v
% O4 P$ d% b! M0 R T% A调用方式如下# R' W+ g$ [) _! w1 m! t
我写了个PlotRegConfInt类函数,方便直接调用绘制两种置信区间图。
6 r- D( R9 H/ i9 fclassdef PlotRegConfInt %-------------------------------------------------------------------------- % @Author: 好玩的Matlab % @公众号:好玩的Matlab % @Created: 09,06,2023 % @Email:2377389590@qq.com % 尊重劳动成果,转载请备注推文链接和公众号名。 % @Disclaimer: This code is provided as-is without any warranty. %-------------------------------------------------------------------------- properties XData; % x数据 YData; % y数据 Type ='prCI' % 绘制方法 % =============【PrCI】===================== % 使用 predict 函数计算置信区间 % 在你给出的 MATLAB 代码中,predict 函数用于计算置信区间,这一计算是基于特定的统计模型(在这里是线性模型) % 和数据。这个方法考虑了数据的整体分布和模型参数的不确定性,并给出了一个关于预测值可能范围的精确估计。 % 1、全面性:它考虑了模型参数的不确定性和数据的内在变异性。 % 2、准确性:使用模型参数的标准误差和协方差矩阵,它可以非常精确地估计预测值的不确定性。 % 3、灵活性:你可以选择不同的置信级别(例如 95%、99% 等) %==============【DeCI】============================== % 使用 yfit +- zValue x sigma 计算置信区间 % 这种方法更为简单和直观,通常用于快速估计预测值的不确定性。它通常假设误差是正态分布的, % 并用标准偏差(δ)来量化这种不确定性。 % 1、简单性:不需要复杂的模型或计算。 % 2、快速性:很容易计算。 % 3、局限性:这种方法通常假定误差是正态分布的,并且不考虑模型参数的不确定性。 Alpha % 置信区间范围' f" t& h- [ k& [0 [* s: I" Y' K
FillColor; % 填充颜色 LineColor; % 线条颜色 FaceAlpha; % 透明度 LineStyle; % 线型 LineWidth; % 线宽 LineMarker; % 标记 end
+ s- e' }# E+ S methods function obj=PlotRegConfInt(sHdl) obj.XData = get(sHdl,'XData'); obj.YData = get(sHdl,'YData'); obj.Type='PrCI'; obj.Alpha=0.95; %默认置信区间 obj.LineColor=get(sHdl,'CData'); % 线颜色 obj.LineStyle='-'; % 线型 obj.LineWidth=3; obj.LineMarker='none'; obj.FillColor=get(sHdl,'CData'); obj.FaceAlpha=get(sHdl,'MarkerFaceAlpha') * 0.5;
8 E5 X, X; ^" T* Z' l end function plotRegConfInt(obj) % 添加对Alpha值的检查 if obj.Alpha 0 || obj.Alpha >=1 disp('置信区间范围在(0,1)之间,请重新设置.'); return;2 x. }$ \5 K$ x/ F
end6 x$ L6 r; U3 ?) R/ O! K/ n
currentAxes = gcf; % 在当前 axes 中搜索 scatter 对象 scatterObj = findobj(currentAxes, 'Type', 'Scatter');
1 A% Z( P C2 ?; h. p+ F % 判断是否找到 scatter 对象 if isempty(scatterObj) scatter(obj.XData, obj.YData, 'r', 'filled', 'MarkerEdgeColor', 'none', 'MarkerFaceAlpha', 0.3); end if isequal(lower('PrCI'), lower(obj.Type))
$ D* O9 N1 X9 }' { % 进行线性回归 linearModel = fitlm(obj.XData, obj.YData); % 计算回归曲线和置信区间 xFit = linspace(min(obj.XData), max(obj.XData), length(obj.XData))'; [yPred, yConfInterval] = predict(linearModel, xFit, 'Alpha', 1-obj.Alpha); % 95%置信区间 % 绘制回归曲线 hold on plot(gca,xFit, yPred, 'color',obj.LineColor, 'LineWidth', obj.LineWidth,'LineStyle',obj.LineStyle,'Marker',obj.LineMarker); % 使用fill函数绘制置信区间%'FaceColor',obj.FillColor, fill(gca,[xFit; flipud(xFit)], [yConfInterval(:, 1); flipud(yConfInterval(:, 2))], obj.FillColor, 'FaceAlpha', obj.FaceAlpha, 'EdgeColor', 'none'); elseif isequal(lower('DeCI'), lower(obj.Type))
/ u. o \0 b& C1 q0 x: g % 使用polyfit进行线性拟合 [polyCoeff, polyStruct] = polyfit(obj.XData, obj.YData, 1); xFit = linspace(min(obj.XData), max(obj.XData), length(obj.XData)); [yFit, fitDelta] = polyval(polyCoeff, xFit, polyStruct); % alpha = 1-obj.Alpha; % 置信区间 zValue = norminv(1 - alpha/2, 0, 1); % 这将返回1.960 % 计算置信区间 upperConfInt = yFit + zValue .* fitDelta; lowerConfInt = yFit - zValue .* fitDelta; % 绘制拟合曲线 hold on plot(gca,xFit, yFit, 'color',obj.LineColor, 'LineWidth', obj.LineWidth,'LineStyle',obj.LineStyle,'Marker',obj.LineMarker); % 使用fill函数绘制置信区间 fill(gca,[xFit, fliplr(xFit)], [upperConfInt, fliplr(lowerConfInt)],obj.FillColor, 'FaceAlpha', obj.FaceAlpha, 'EdgeColor', 'none'); else disp(['没有此绘制回归+置信区间的属性',obj.Type,'目前只有DeCI 和PrCI绘图方式']) end end endend其中参数如下,详细参数介绍在代码中XData:x数据YData:y数据 Type:绘制方法 Alpha:置信区间范围 FillColor:填充颜色 LineColor: 线条颜色 FaceAlpha:透明度 LineStyle:线型 LineWidth:线宽 LineMarker:标记1 p* i: b1 @- @9 S: A& f: R
& z. v! ^. r/ r$ ?6 {
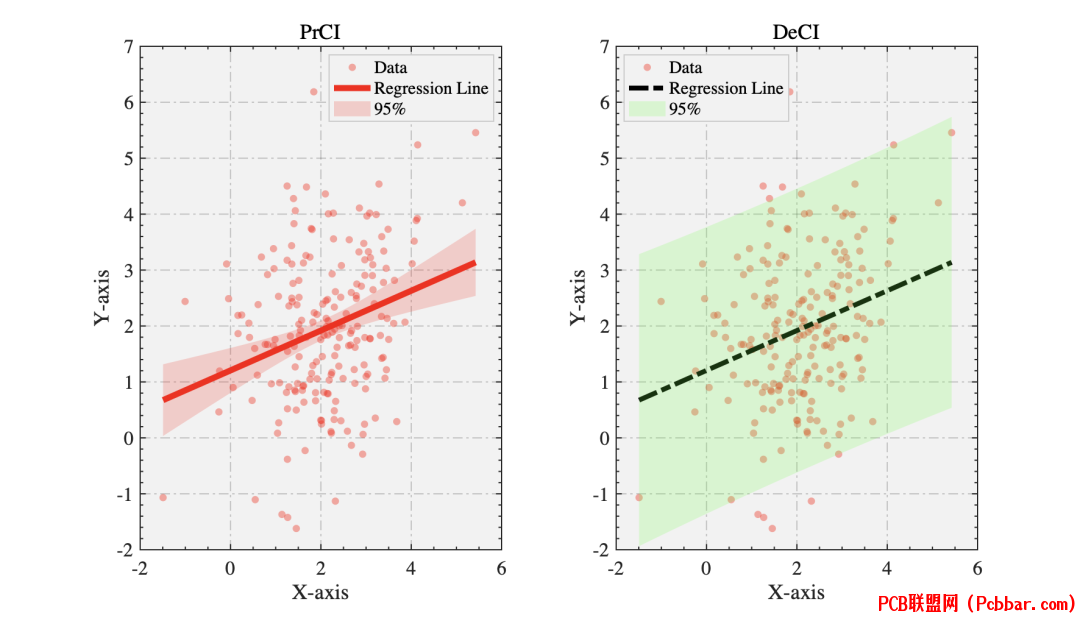
PlotRegConfInt函数调用方法
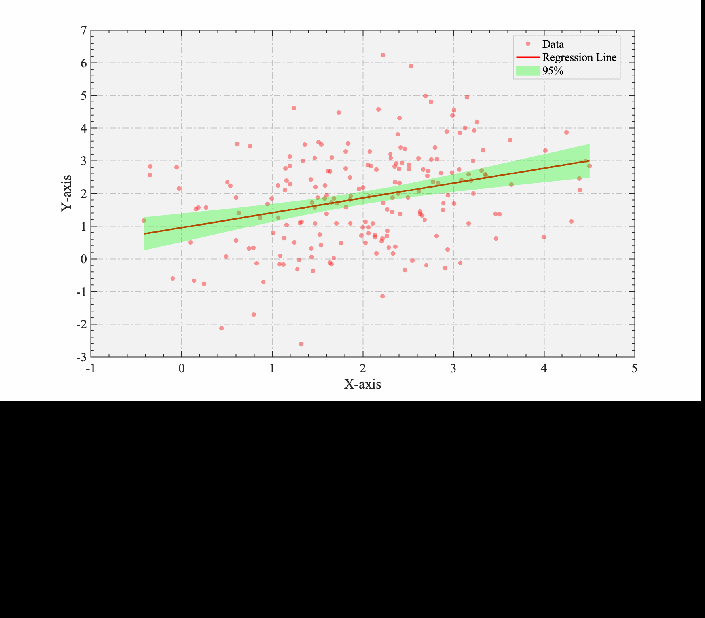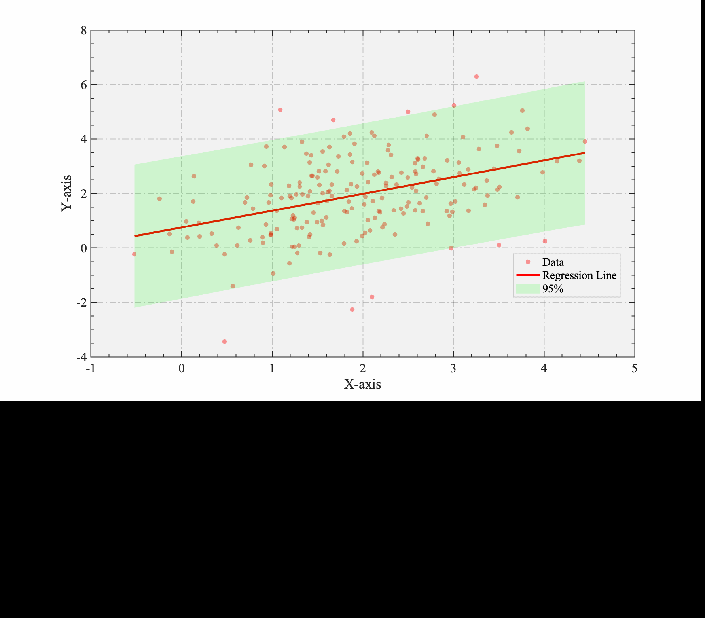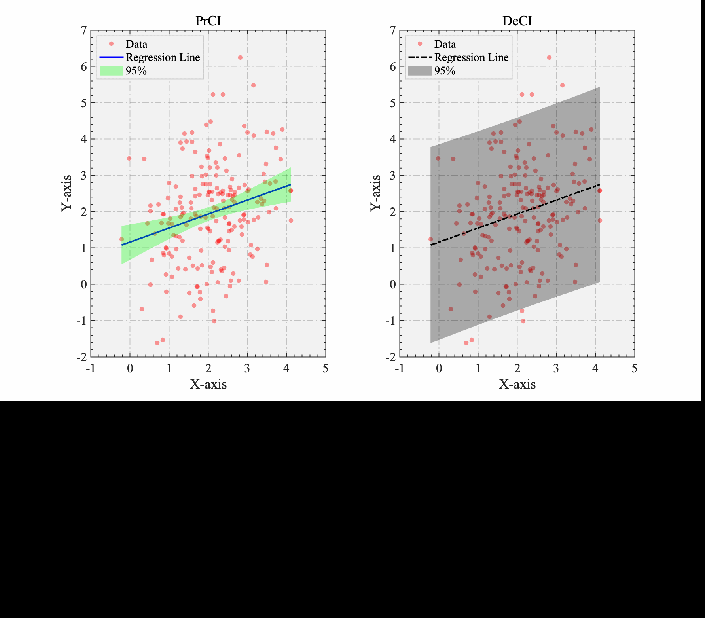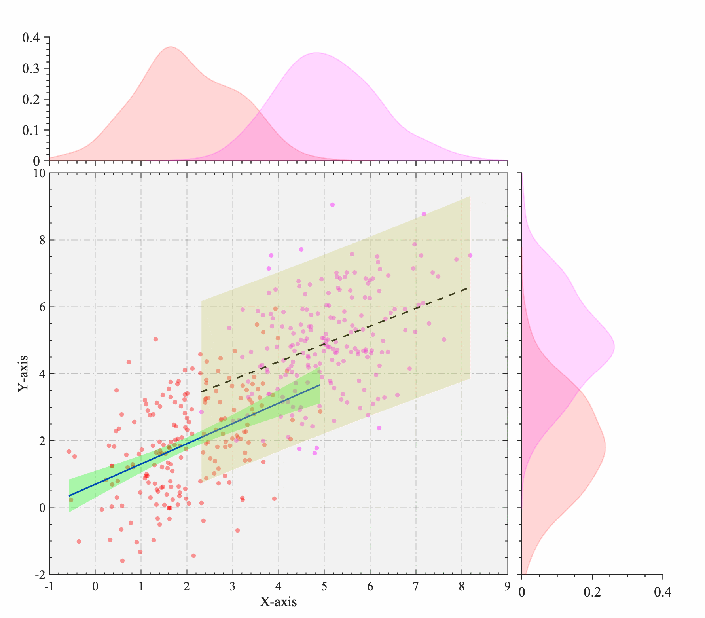
% ]9 g9 }/ D; |' a) P2 F1 rclc;clear;close all;%--------------------------------------------------------------------------% @Author: 好玩的Matlab% @公众号:好玩的Matlab% @Created: 09,06,2023% @Email:2377389590@qq.com% 尊重劳动成果,转载请备注推文链接和公众号名。% @Disclaimer: This code is provided as-is without any warranty.%--------------------------------------------------------------------------% 使用提供的数据data = repmat([2 2], 200, 1) + randn(200, 2) * [1 .5; 0 1.32];xData = data(:, 1);yData = data(:, 2);% 绘制散点图figure('Position',[383 355 886 507]);subplot(1,2,1);sHdl=scatter(xData, yData, 'r', 'filled', 'MarkerEdgeColor', 'none', 'MarkerFaceAlpha', 0.4);hold onP1=PlotRegConfInt(sHdl);P1.Alpha=0.95;% P1.LineColor='b';% P1.LineWidth=2;P1.plotRegConfInt();defaultAxeslegend(gca, 'Data', 'Regression Line','95%','Confidence Interval','box','on','Location','best','EdgeColor', [1 1 1]*0.8);# k. ~4 w9 e' z/ P
title('PrCI')subplot(1,2,2);sHdl=scatter(xData, yData, 'r', 'filled', 'MarkerEdgeColor', 'none', 'MarkerFaceAlpha', 0.4);P2=PlotRegConfInt(sHdl);P2.Type='DeCI'; %设置两种绘制置信区间的方法P2.Alpha=0.95;% 设置置信区间P2.FillColor='g';% 设置之前区间填充的颜色P2.LineColor='k';%回归先颜色P2.LineStyle='-.';%回归先样式P2.LineMarker='none';P2.LineWidth=4; %回归线粗细P2.plotRegConfInt();
9 ^0 r, `/ d1 J* Q: fdefaultAxeslegend(gca, 'Data', 'Regression Line','95%','Confidence Interval','box','on','Location','best','EdgeColor', [1 1 1]*0.8);title('DeCI')! n. t" p2 ^* P R/ I$ R
0tjiqbi2ano6405196344.png
! g3 Z; x b ^6 [% b
. S1 f6 A/ S x% ?: F- p% C' {3 Q& ^' [6 z
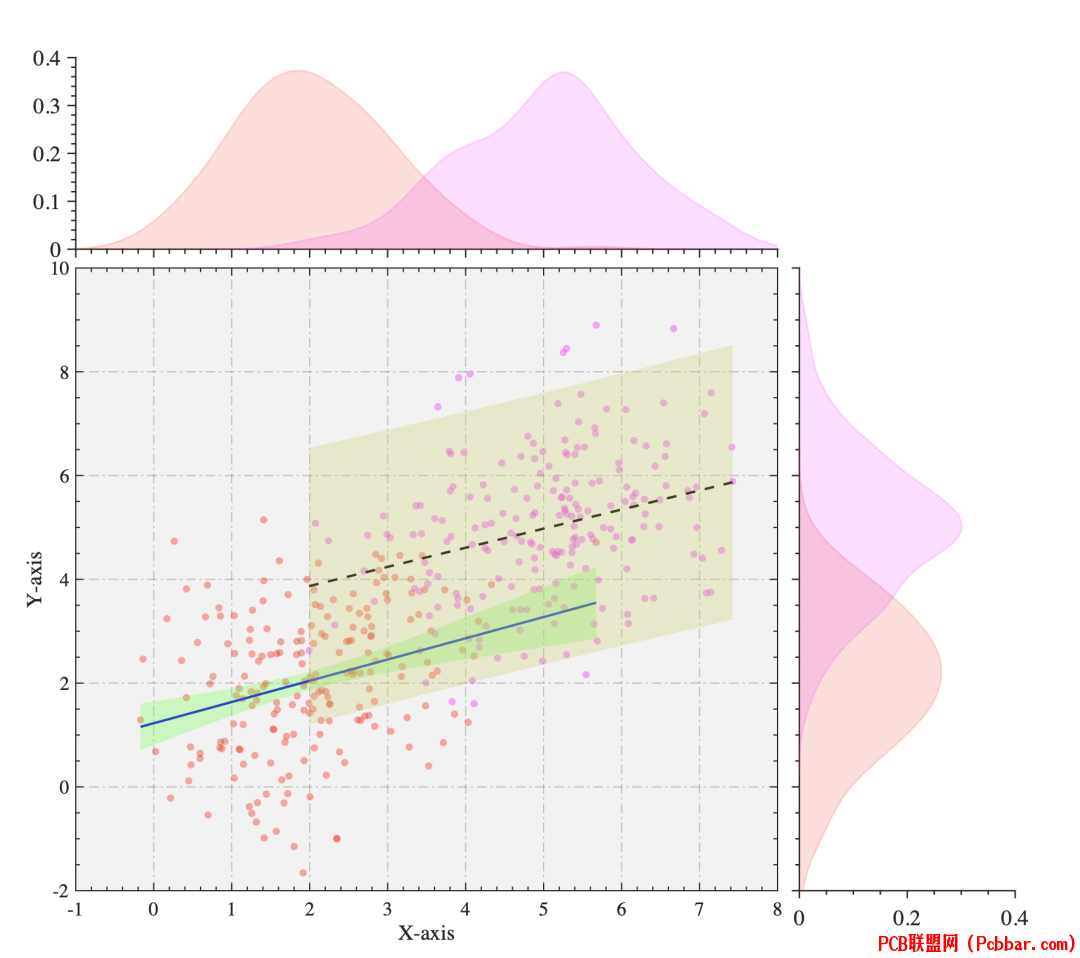
添加边际图+核密度图. Q" X4 s: u H$ y$ W2 ?7 I
clc;clear;close all;%--------------------------------------------------------------------------% @Author: 好玩的Matlab% @公众号:好玩的Matlab% @Created: 09,06,2023% @Email:2377389590@qq.com% 尊重劳动成果,转载请备注推文链接和公众号名。% @Disclaimer: This code is provided as-is without any warranty.%--------------------------------------------------------------------------% 使用提供的数据data1 = repmat([2 2], 200, 1) + randn(200, 2) * [1 .5; 0 1.32];data2 = repmat([5 5], 200, 1) + randn(200, 2) * [1 .5; 0 1.32];xData1 = data1(:, 1);yData1 = data1(:, 2);1 P. ^& ^, Y R- Y) {2 U
xData2 = data2(:, 1);yData2 = data2(:, 2);% 绘制散点图figure('Position',[383 355 886 507]);hold onsHdl1=scatter(xData1, yData1, 'r', 'filled', 'MarkerEdgeColor', 'none', 'MarkerFaceAlpha', 0.4);sHdl2=scatter(xData2, yData2, 'm', 'filled', 'MarkerEdgeColor', 'none', 'MarkerFaceAlpha', 0.4);defaultAxes% 绘制回归线置信区间P1=PlotRegConfInt(sHdl1);P1.LineColor='b';P1.LineWidth=2;P1.plotRegConfInt();P2=PlotRegConfInt(sHdl2);P2.Type='DeCI';P2.FillColor=[1,1,0.5]*0.8;P2.LineStyle='--';P2.LineColor='k';P2.LineWidth=2;P2.plotRegConfInt();
2 U f0 L) v3 v/ X I, [% 设置边际组图Phdl1=PlotDensFill(sHdl1);Phdl1.plotDensFill();; _ ?' h8 r1 a* U8 r
Phdl2=PlotDensFill(sHdl2);Phdl2.plotDensFill();* ]( j! O4 [# F
h5c2fbv43jh6405196444.png
 3 _: Y0 m, p/ g+ a9 t8 J
3 _: Y0 m, p/ g+ a9 t8 J
0 q+ h& b: o2 |0 d! P# b- -THE END- -
0 P. m( Z* N0 V2 S* b' R
, j. h- {( I# }0 C& M% ~8 N源码下载:gitee下载:https://gitee.com/iDMatlab/PlotRegConfInt- G/ U0 w `: t3 ]$ Q, M' a5 O
rsidfbp34km6405196544.png

- ^% S2 X) L8 a/ t' A& Z参考资料:【1】贾俊平《统计学》【2】https://zhuanlan.zhihu.com/p/416569320?ivk_sa=1024320u&utm_id=0【3】https://www.mathworks.com/help/releases/R2021b/stats/fitlm.html【4】https://www.mathworks.com/help/releases/R2021b/matlab/ref/polyfit.html【5】MATLAB|聚类散点图|边际图|核密度填充图
. j. x( f4 g% P5 X' Y扫一扫加QQ群! `; i; J, q; m1 t/ t6 N8 [
2tzs0eaheue6405196644.jpg
 , u6 Z1 @0 I( W8 h
, u6 Z1 @0 I( W8 h
扫一扫加管理员微信
5 M( r" h) h2 L' K5 U+ q
zknrlikz0xw6405196744.png

& \- S+ W1 r8 V* |( D% o! L
u2mntaxein06405196844.jpg

|
|