【摘要】
4 C8 P- @' |5 E目前大家设计得最多的莫过于高速数字芯片及相关电路设计和应用,对模拟的电路部分的设计涉及得很少。这里简单介绍一下高带宽低噪声跨阻放大器(TIA)应用电路的噪声估算方法,主要涉及的参数有带宽、增益及噪声。- i; P4 q" i: k' m9 A0 I; |
一、引言
* Z. o5 }; H* r$ g: H* B1 W1 n尽管目前很多模拟电路都集成到芯片的内部,只留了少量的电阻电容之类的元件在外面,减少设计的难度,但还是会有少数应用电路需要用到模拟芯片,比如说做一块处理微弱的模拟信号的评估板,需要放大好几级,没有专用芯片进行放大,就只能用模拟器件去搭建。对于微弱的信号,其信噪比是非常关键的参数,决定了小信号是否能检测出来。提高信噪比的重要方法是将低噪声,所以我们设计此类电路必须要对噪声进行估算,选择性价比合适的芯片,以提高设计的性能。这里简单介绍一下高带宽低噪声电路的噪声估算方法。9 r9 C4 P: m1 H; L& s3 Q8 F
二、光电二极管+低噪声跨阻放大器的噪声估算1 I1 D: G- f7 H9 G
在光通信应用中,用得最多的两种光电二极管是PIN和APD。由于这种光电二极管产生的电流都很小,所以不能用一般输入噪声大的跨阻放大器直接处理。在实际应用中要求放大器具有高带宽、低噪声、高增益的性能,以便检测出微弱的信号,增强信噪比及信号质量、减小误码率,提高动态范围。
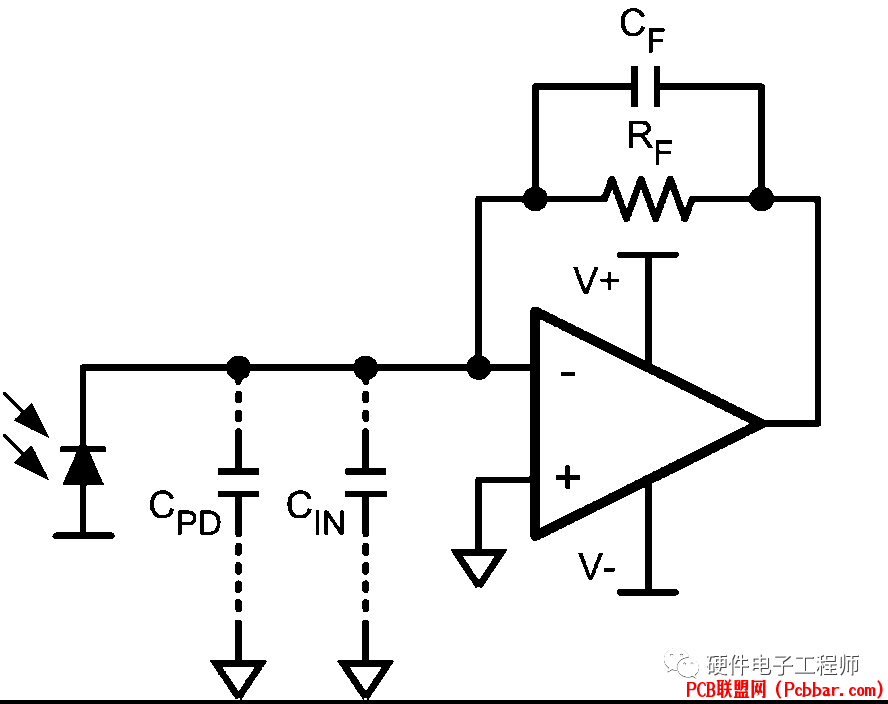
x2 Z, O+ ~6 h8 ]7 K& y, L; @+ p以下是工程中一典型的电路,电路主要由光电二极管和跨阻放大器组成。
2 e+ T: }0 y6 i) W+ L! H% PCpd---为光电二极管自身的电容,6 p; ]5 `2 }+ k
Cin---为放大器输入电容,
5 X5 f) n$ u; u7 L" ARf---为跨阻,将电流转化为电压,
7 e6 T4 l1 y' `, WCf---为相位补偿电容。; P& C, m. W2 |; n5 ]8 Y( y
k3poe0habze64024258328.png
; Z6 V7 _! y' K* j6 J: Z信号的-3dB带宽为:
1 G6 w# f3 x0 W* f5 r+ q3 r
ojuhqebia4164024258428.jpg

: g4 r7 j4 b: E) y* c2 L8 O1 k其中,GBP为带宽增益积. f' n; w! d; Q* y
Ct为Cpd、Cin之和, ~6 L7 z. k v9 P% d
为了使电路稳定,最佳相位补偿电容的值为
7 y5 ?) n* y# b7 M+ z
bvw0guvmnjg64024258528.png
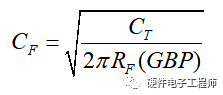 1 {, O$ g+ f/ a, {% P8 v8 M
1 {, O$ g+ f/ a, {% P8 v8 M
等效输入噪声电流为
9 q6 `+ |+ P2 P, G& u! q
srqehodbza564024258628.png
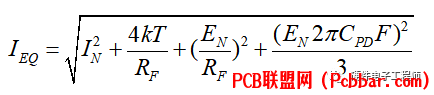 5 c: S. [+ T) M8 Y* |
5 c: S. [+ T) M8 Y* |
其中,In为放大器反向输入端的电流输入噪声
* \: X; Y4 t# _. v; R% ? En为放大器的输入电压噪声$ r& Z/ E6 J3 _0 X& U( f
Cpd为光电二极管的电容7 ]+ {8 }( X9 q; P" P
F为链路的信号频率
! b8 i6 W! o8 w& i, X9 |
fxx5rhnmslz64024258728.png

$ V: f# w2 K" u; ^# A0 x7 HTIA输出的均方根噪声电压为:3 l3 o: w& k4 w& L4 q8 Q
140340eowue64024258828.png
 2 p T# j# V: ?" B" i) W4 s
2 p T# j# V: ?" B" i) W4 s
其中,
* T: Q9 R( k/ [* w. u& W4 {5 ?I^2npd为光电二极管的均方根噪声电流
: t* P: m9 j; Q( x: b5 yF为放大器输出的带宽
$ ^8 g2 f, A% m7 }设APD输出有用信号电流为Ipd
7 n5 w) h/ R% `5 p1 @7 d9 ~, L% B,则其信噪比为:
, X; w @( S6 ~5 ?. S, \2 t- L
qkjs0av0bkv64024258928.png
 & v; z2 z' f# I: l& K0 l: P1 C
& v; z2 z' f# I: l& K0 l: P1 C
三、结论
; e- B6 }3 l- J! B/ A2 M1 v0 w此电路的设计时要注意的几点:为了得到更高的带宽和增益,需要选择带宽增益积大的芯片,Rf越大,增益越高;为了得到更高的信噪比,需要选择输入电压/电流噪声小的芯片,另外,如果在带宽允许的前提下,可以适当降低带宽,增加Rf。3 @: t4 R' K/ J% C( }
四、总结
, I2 C2 U/ W$ L3 B. d利用上述的几个公式,我们很容易就能估算出TIA电路的噪声范围,对放大器的选型、后端电路的设计及误码率的计算具体一定的参考意义。 |