|
|

引言
/ G) r& }- Y" o可编程光电子线路是量子信息处理、机器学习加速和光信号处理等多种应用的关键技术。随着这些线路不断扩大以满足更复杂任务的需求,面临着与其基本构建模块——相移器——相关的独特挑战。与电子线路中的晶体管不同,相移器无法在不影响性能的情况下任意缩小。本文探讨了优化多端口干涉仪以实现相位高效可编程光电子技术的最新进展,推动这些系统向信息理论极限迈进[1]。
, M9 L: [4 Z( P$ L* ^. `" C/ Y J! z$ i
ojmq2yldduo64068665417.png
 9 u! ]6 y/ s3 Q- X6 b4 ^
9 u! ]6 y/ s3 Q- X6 b4 ^
8 P; l, ?+ @" s' t+ z& {! c' H4 _' i理解挑战) z _8 ^: R! Y
传统的光电子线路扩展方法主要集中在器件级改进上,如减少马赫-曾德尔干涉仪(MZI)和相移器的功耗和占用面积。然而,最新研究表明,系统和架构级的选择对整体性能和可扩展性同样有重大影响。
5 I u# @8 w7 g; ^+ ~- i1 t. N
2 w, ~5 V# y3 S% K. ^2 Q9 i7 C7 D6 e主要挑战在于相移器设计中固有的权衡。例如,热光相移器通常需要约20 mW的功率才能实现π相移。降低功耗往往会以降低速度或增加尺寸和插入损耗为代价。相变材料(PCM)和金属氧化物半导体电容器(MOSCAP)等替代技术虽然功耗低,但会引入与相位相关的光学损耗。% d) W* H8 T1 ~ X/ O2 A# K
& b+ S- j( O/ q9 N8 x; F3 U( ]' C这些权衡因素对可编程光电子线路的扩展构成了实际限制,导致现实实现的线路比光波长设定的理论最小值大10-100倍。
, V0 R3 N2 l! X$ T+ q/ e: k2 ]' Z3 N; K
追求相位效率9 x% L' T' H2 N' `
为应对这些挑战,研究人员开始探索"以少胜多"的方法,创建能够最小化大型线路中每个元件平均相移的架构。这种方法旨在绕过实现大相移相关的权衡,同时保持线路的功能性和可编程性。
! p) p# x0 H) N2 w, u: |, T& x# H+ G! z; u2 R# `
信息理论界限
' `& z) I4 E e% o, ]4 }在深入探讨具体架构之前,了解多端口干涉仪中相位效率的基本限制很重要。研究人员利用信息理论推导出了光电子线路通用性所需的平均相移下限。+ @' B" e9 z+ C- p& T& q' R) W
' @+ B0 A4 B' H6 [+ F! N8 |: R
z0cqiceuhwq64068665517.png
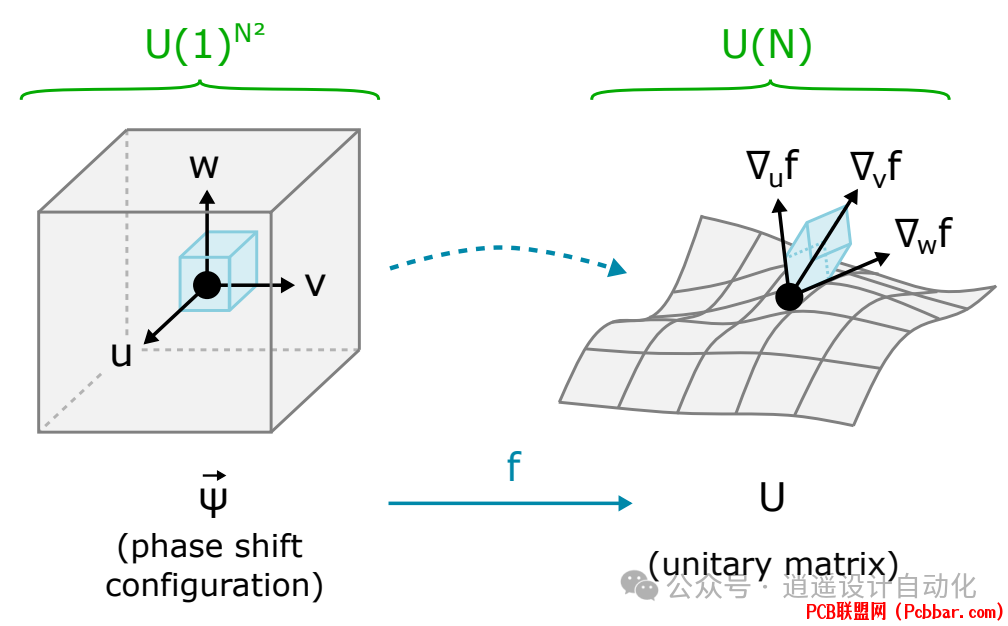
4 l& Q, m& O# L2 v. U3 f图1:多端口干涉仪实现的映射 f : ψ → U 的可视化,其中单位体积 dVψ 映射到由梯度向量 ?ψm f 张成的平行六面体,体积为 dVU = |?(U)/?(ψ)|dVψ。
: l; q8 u6 } ^+ o6 A% N0 `: h: U$ h+ a- y
这个界限随着干涉仪输入和输出模式数 N 的增加而按 O(1/√N) 缩放。这个缩放定律为优化线路架构提供了目标,并为评估不同设计的效率设定了基准。2 [/ m/ E* N ` q5 R3 z2 V4 ^
7 M, A' V* o; M7 c& D
MZI网格:起点3 J. q* ?9 O( ?0 D1 P1 U6 {' {
构建通用多端口干涉仪的传统方法使用马赫-曾德尔干涉仪(MZI)网格。虽然有效,但这种架构在相位效率方面未能达到理论界限。/ C8 X8 l9 N, I1 l& m
0 }# J) k& c# E! u
egcuzkpdzyi64068665618.png
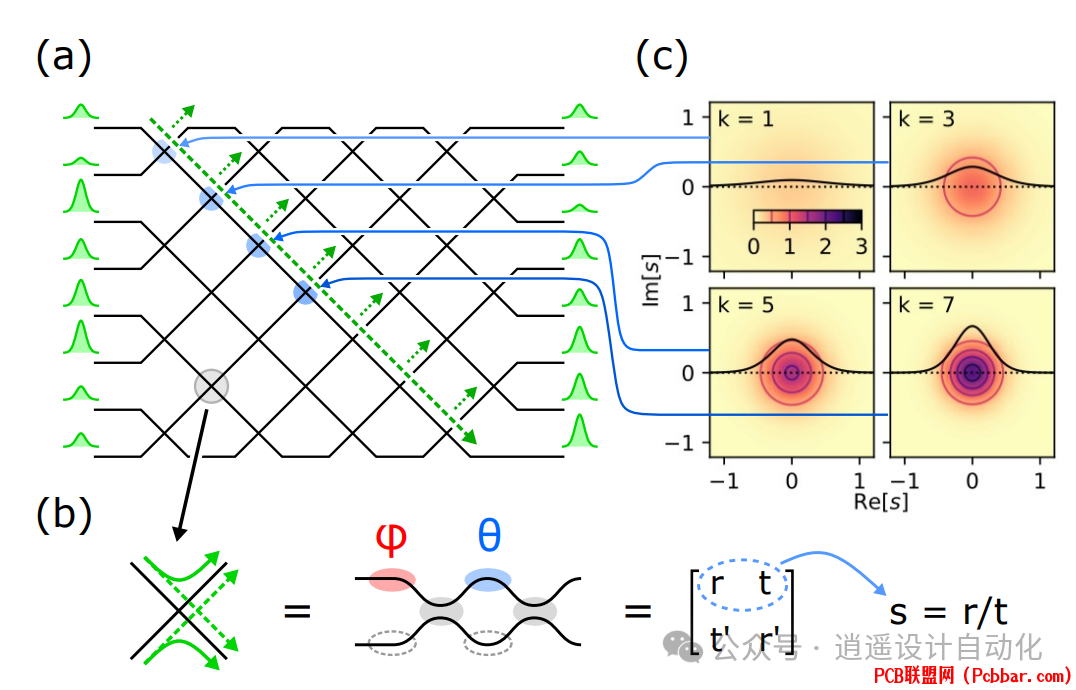
7 f; c* [+ _* H图2:(a) 8 × 8 Clements网格,由可调交叉点的矩形阵列组成(相位屏幕为清晰起见省略)。(b) MZI交叉点及其由2 × 2矩阵T(方程(10))表示的分裂比s。(c) 对于Haar均匀分布的酉矩阵,等级为1、3、5和7的MZI的P(s),显示分布如何随着向网格中心移动而集中。
4 E2 r% |* U6 N# O+ h" O5 K8 C, `$ l+ O8 f0 y2 o; N3 }
在MZI网格中,随着线路规模的增加,平均相移保持恒定(O(1)),与信息理论界限预测的O(1/√N)缩放显著偏离。这种低效限制了基于MZI的线路随规模增大而扩展的能力。7 { U# r/ U1 Z% ?( R ]
2 c, Q: E! q8 g" e% c" L
3-MZI:迈向效率的一步
" c2 h* D. [! ~% f0 q为解决标准MZI网格的局限性,研究人员提出了一种称为3-MZI的替代设计。这种架构由标准MZI加上一个包围外部相移器的额外50:50分束器组成。
$ N, m/ V; f! v5 H5 j& M. p4 Q' P* H* z5 b' z( {% X1 N
s22ihnm3op564068665718.png
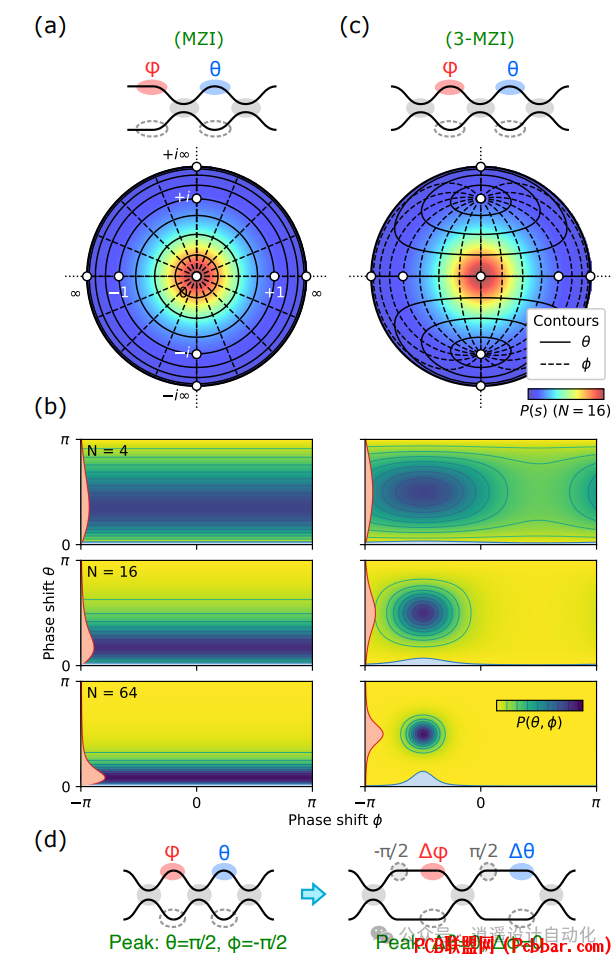
6 g1 Q) ?5 d9 l图3:(a) 标准MZI交叉点,通过极坐标将(θ, φ)映射到s。绘制了N = 16网格的概率P(s),显示了靠近s = 0的浓度。(b) P(θ, φ)随网格大小变化的概率,显示θ受限但φ不受限。(c) 3-MZI交叉点,在s = 0附近的映射在局部上是笛卡尔的,并且限制了θ和φ。(d) 利用制造过程中引入的相位偏移将分布P(θ, φ)集中在零附近。# ^+ S j1 X: H3 L9 e. w2 o# M
3 e8 _. G$ n( U
3-MZI设计提供了几个优势:
9 c5 e8 V) B2 X, Q9 Q1. 改进的缩放:3-MZI网格中的平均相移按O(1/√N)缩放,与理论界限相匹配。
* Z) x* j5 X' L) h6 }! g# F2. 受限分布:内部(θ)和外部(φ)相移都紧密地限制在其交叉状态值附近。
+ o, K* L- H7 \1 l" @3. 制造优化:通过在制造过程中应用物理相位偏移,可调相移器只需实现小的残余项。
' ^. U; v7 t! W5 r; i- y# |5 E
, ~- l2 F" u/ ?, t# l数值模拟和理论分析表明,3-MZI架构接近信息理论界限的2-3倍以内,相比标准MZI网格有显著改进。& Y5 z' j8 X& h K
7 W* D* `6 Q9 L3 u( P
bvodq4gmqxv64068665818.png
 + }8 z" \; \& N! s
+ }8 z" \; \& N! s
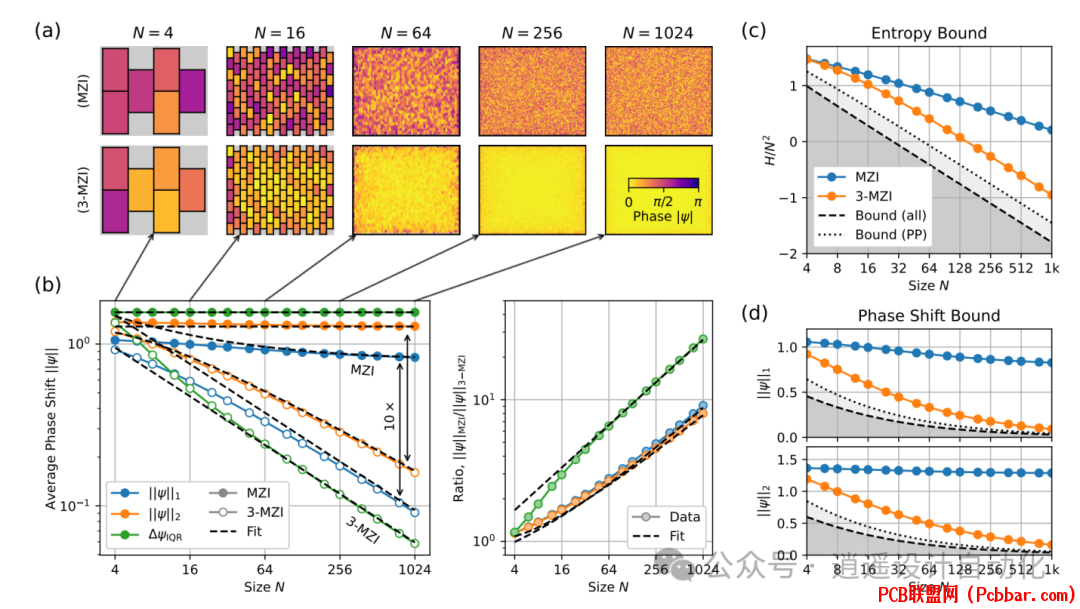
图4:(a) 大小为N = 4-1024的网格可视化,编程实现特定Haar均匀采样矩阵,其中MZI根据平均相移|ψ| ≡ 1/2(|θ| + |φ|)着色。(b) 相移矩作为网格大小的函数图(左)和每种矩类型的MZI/3-MZI比率(右),说明了后者网格类型的优势。(c) MZI和3-MZI网格的每自由度熵,与信息理论界限比较。绘制了通用和推拉(PP)界限。(d) 相移矩与界限的比较。 R3 }6 @; Q& u+ q* i% c% M2 i
?; `8 L( U- ~" A
对于实际网格大小(N ≈ 256),3-MZI设计在平均相移方面比标准MZI网格减少了10-20倍,具体取决于所选择的优化指标。
; m' {! Q4 K4 H- y7 e
' m6 z4 b* t2 Y7 M# a4 Z! y2 B5 t
`0 ~* {5 Y7 v2 B9 C) I超越酉矩阵:高斯分布
: }0 ]- ^. Q% k3 k围绕多端口干涉仪的大部分理论都集中在酉矩阵上,但许多实际应用涉及非酉变换。研究人员已将分析扩展到涵盖高斯分布的目标矩阵,这在信息处理任务中很常见。1 G& c$ H1 u5 c7 g
9 w; K; V) k5 B: c+ t) Y3 `$ _
对于这些非酉应用,基于交叉架构的设计,如菱形和PILOSS(路径无关损耗)设计显示出了前景。当与3-MZI交叉单元结合时,这些架构可以对小条目的高斯分布矩阵达到信息理论界限。
2 x$ {7 x, H/ Y' \3 y; K; p( [9 L& p$ d& {4 J8 T+ [
x1cl35h2rav64068665918.png
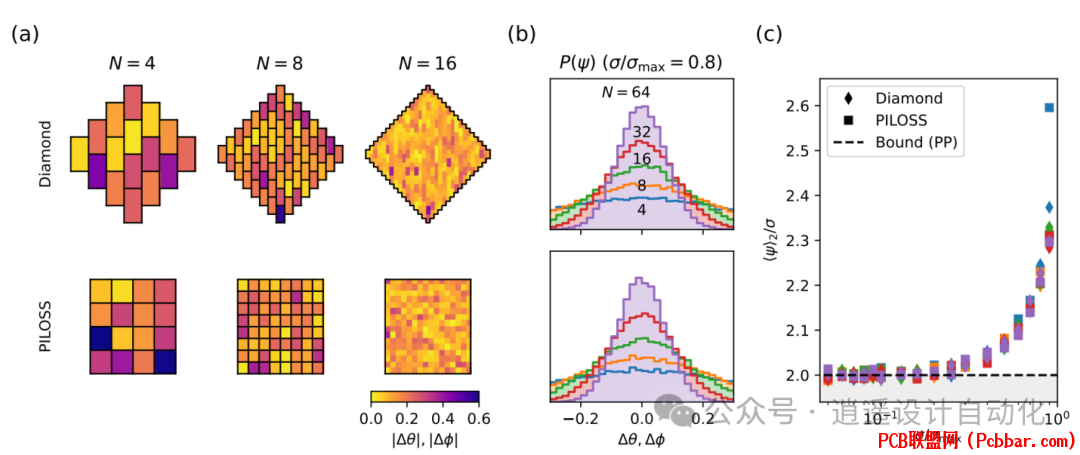 6 V( k( m# H) t! n; m
6 V( k( m# H) t! n; m
图5:具有高斯随机目标矩阵的非酉网格。(a) 菱形和PILOSS网格的相移Δθ, Δφ,目标矩阵随机采样,σ/σmax = 0.8。(b) 相移分布作为网格大小的函数,显示与?ψ? ∝ 1/√N一致的方差减小。(c) L2平均相移作为σ/σmax的函数,与(推拉)信息理论界限?ψ?2 ≥ 2σ比较。$ n% z0 O4 F5 ~6 D4 X. u. N* ]- ~
1 e( ]. _% U& k* C% Y1 N5 w这些结果表明,相位高效设计不限于酉变换,可以扩展到与实际应用相关的更广泛的矩阵操作类别。# O" ]* O4 O! u
( _8 |7 b6 N( w; t" h
实际意义:L∞约束下的神经网络训练 q! K: W c9 K% ~
平均相移是整体效率的重要指标,但许多实际实现面临着每个元件可达到的最大相移的"硬"上限。这种约束在光学深度学习应用中尤为相关。6 w8 b. |! B( F
/ M2 U9 r- {$ M! p5 T: p( a9 r
为探究这些约束的影响,研究人员调查了L∞约束下光学神经网络的训练,其中最大相移被限制在一小部分弧度内。
1 e5 k/ k7 Z2 Z" n6 R
7 W" |" l7 x% P
besu5x1pahn64068666018.png
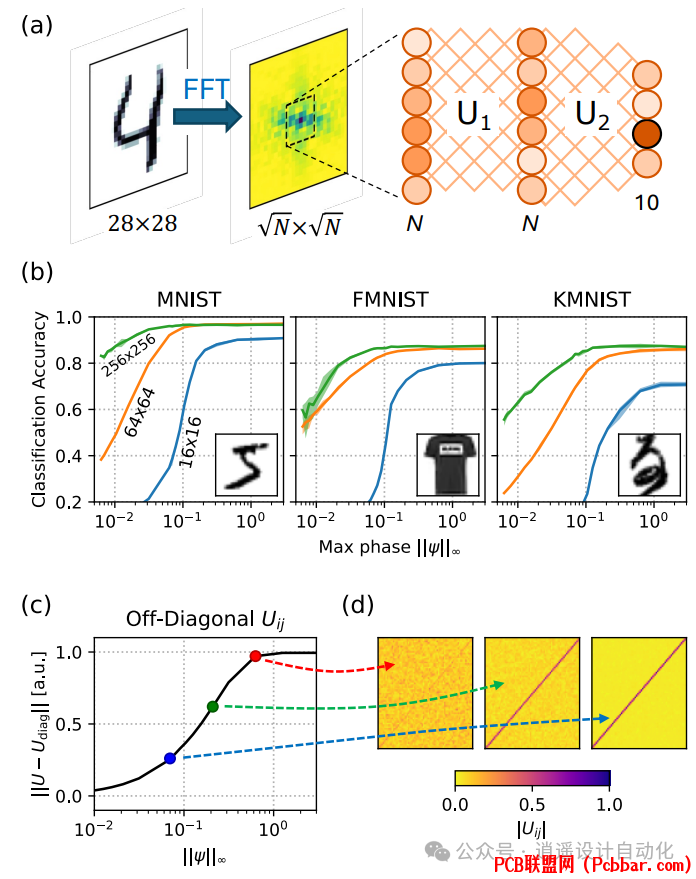 5 Y- q, r! Q$ Z j1 K4 Y
5 Y- q, r! Q$ Z j1 K4 Y
图6:相位约束ONN训练。(a) ONN架构。FFT和裁剪是预处理步骤,而N × N可训练层U1和U2用Clements网格实现。(b) MNIST、FMNIST和KMNIST分类准确率作为层大小N和最大相位||ψ||∞的函数。(c) U1的矩阵范数中非对角元素贡献的分数,作为||ψ||∞的函数。MNIST,N = 64;U2的曲线类似。(d) 来自(c)的代表性矩阵,显示当||ψ||∞较小时,反对角线周围的聚集增加。8 q2 j Y/ X! V: w5 K
3 h) m* P& q7 q2 ^' o% Y' Z# D7 U令人惊讶的是,这些研究表明,即使最大相移被限制在一小部分弧度内,光学神经网络也能训练到达到与无约束模型相当的准确度。这一发现表明,L∞约束训练可能对使基于网格的光学神经网络能够扩展很重要,特别是在面临严重VπL权衡的快速平台(如LiNbO3或压电光机械系统)中。$ \+ X* `% ?" r# B! _( N
% |1 z5 h$ C1 ^2 p; \. }
未来方向和开放问题- R d6 e5 [0 F0 V% v
随着可编程光电子技术领域的不断发展,出现了几个开放问题和未来研究方向:
8 n7 _5 w4 u5 [1. 过完备基:将信息理论分析扩展到相移器数量多于严格必要的系统。
/ M$ U0 L6 @0 a( }2. 替代架构:探索非MZI基础设计(如MPLC、FFT和其他新型方法)的相移统计。
4 X i9 G/ K* S* a" G3. 连续系统:研究多模波导的使用,以及它们如何突破集中元件相移器的假设。+ q4 y- m) Z7 c" T2 H
4. 硬件缺陷:研究相位高效设计与现实、不完美硬件的错误纠正策略之间的相互作用。
( }! l, N" d9 X/ G5 b' P( l
7 U' A: ~% S1 b2 O结论4 y) L% D$ x: ~3 c0 C, f
追求相位高效的可编程光电子技术代表了扩展光信息处理系统方法的重大转变。通过将相移视为需要节约的资源,研究人员发现了新的线路设计范式,有望推动大规模光电子系统的可能性边界。
! u3 P+ X ^% s1 {4 ~. j; f: ]
7 Z6 ]4 q7 P! G特别是3-MZI架构已成为通用多端口干涉仪的近乎最优解决方案,与传统设计相比,在相位效率方面提供了数量级的改进。当与用于非酉操作的基于交叉架构的布局结合时,这些进展为能够处理日益复杂的量子计算、机器学习和信号处理任务的新一代光电子线路奠定了基础。 _1 ?$ o5 |1 p
" h: k; U, G- ~, [! k随着该领域不断发展,理论界限、架构创新和实际约束之间的相互作用将推动向真正大规模可编程光电子技术的进一步进展。通过推动相位效率的极限,研究人员正在为光信息处理开辟新的可能性,有朝一日可能在功率和能力方面与电子对应物相媲美或超越。% n& g# t: x# }1 Z
. g: d! W* ~9 P. R0 m2 p: p6 M
. Z$ ]- p0 J9 y参考文献( b2 Q' q. N" N) M( k( C
[1] R. Hamerly, J. R. Basani, A. Sludds, S. K. Vadlamani, and D. Englund, "Towards the Information-Theoretic Limit of Programmable Photonics," arXiv:2408.09673v1 [physics.optics], Aug. 2024.$ v$ `7 Y" B p6 F( X4 T# y. R& b' f a
) L7 i7 g5 ? ^0 W- i- END -. C# i( e' Z( H6 R7 s, S' W1 }- X& O
F" ?% ^+ `( \7 F$ [- }6 r
软件申请我们欢迎化合物/硅基光电子芯片的研究人员和工程师申请体验免费版PIC Studio软件。无论是研究还是商业应用,PIC Studio都可提升您的工作效能。
, G5 U% E/ O7 A" h7 K0 i点击左下角"阅读原文"马上申请
" [7 L1 Q% q' Q# E+ I$ M! u9 a4 J
8 w* G3 g8 G0 v% N欢迎转载
( T; u% s2 ?! e. H- P( ~( ] r( F3 u% p
转载请注明出处,请勿修改内容和删除作者信息!2 q2 p# W8 G$ F6 g3 t4 s" Y' c
) i; m* L2 P- ~4 N: s! \$ H( w/ M+ U3 O% n. O [' }
: w6 c) w2 m( K
zsg4i5k1vpl64068666119.gif
' {0 c5 q; @8 }/ O& h e
0 Z! x. | G0 h; E% G3 ?关注我们
/ p, s" Y" x. ~7 k/ q4 _1 H+ k
4 y7 I6 g8 F3 q+ ~# R! k. n
et4ge1d5qtz64068666219.png

. }( ^$ K4 q6 u; R- S4 ^ |
" M* n1 s* `" K4 W
3xvdetv15p564068666319.png
 * T7 b% [$ m3 Y# S5 {6 D- H1 m5 y
* T7 b% [$ m3 Y# S5 {6 D- H1 m5 y
|
6 m* P+ Y: W/ ?7 Q* _/ t
ntjcpczmhzs64068666419.png
 3 L% C& G* |: S9 j; R
3 L% C& G* |: S9 j; R
|
% a( b4 H$ g5 l" Y
. @! `0 ?& F8 I) o# `* x1 P4 r% e5 B4 [7 X2 c
y Z# t4 ?! u& Z/ @
关于我们:
; F* G5 J: u! f. i! Z6 P- v深圳逍遥科技有限公司(Latitude Design Automation Inc.)是一家专注于半导体芯片设计自动化(EDA)的高科技软件公司。我们自主开发特色工艺芯片设计和仿真软件,提供成熟的设计解决方案如PIC Studio、MEMS Studio和Meta Studio,分别针对光电芯片、微机电系统、超透镜的设计与仿真。我们提供特色工艺的半导体芯片集成电路版图、IP和PDK工程服务,广泛服务于光通讯、光计算、光量子通信和微纳光子器件领域的头部客户。逍遥科技与国内外晶圆代工厂及硅光/MEMS中试线合作,推动特色工艺半导体产业链发展,致力于为客户提供前沿技术与服务。" N1 {2 D" @! O5 D' r
# B$ n, I, ?$ n6 u3 B5 Z* ^% [http://www.latitudeda.com/! d8 q0 O$ p3 W& | e1 i; I
(点击上方名片关注我们,发现更多精彩内容) |
|