如何选择CRC校验码的长度？

电子设计联盟

vtpp4vvsgfj64044431419.gif

% W+ M  D8 w: _1 Y+ {! W点击上方蓝色字体，关注我们
. O1 P. l& w" R" ]
选择CRC校验码的长度时确实需要在检错能力和系统开销之间做出权衡。CRC码的长度（通常是4、8、16、32位）直接影响到能检测到的错误类型和概率。

0tnvlapkqrq64044431519.png

要确定在一定检错概率 p 下的最小CRC长度，可以从几个方面入手，包括信息长度 n、错误检测概率需求 p、以及CRC多项式的选择。
, e; x* ^  Q( V
2 n$ E: w' D( L! m$ N下面从理论背景、实用方法以及计算步骤等方面详细解释。
1
5 H, o# |" L3 @; Y* N, i( E9 o) b理论背景：CRC的检错原理
CRC（Cyclic Redundancy Check）使用一个特定的生成多项式对数据帧进行余数计算，产生一个校验码。
! p+ u- Z. Z/ q: Q, {2 ^
# ~7 b4 q3 T7 Q  h接收端利用相同的多项式重算余数，如果余数为零则判定无误差，否则判定出错。
+ u+ Z' q" X" |/ l" w
9 D, s2 @1 |% E: F# x3 B2 u: d对于不同长度的CRC码，其生成多项式能探测不同类型的错误：
, W9 E0 A/ l; W' J# \: k/ q) F0 W1 _

单比特错误：任何CRC都能检测单比特错误。

连续位翻转的突发错误：长度为 k 位的CRC最多可以检测到长度不超过 k 位的突发错误。

随机错误：概率与CRC码的位数有关。

( i8 ]7 v, z8 N! Q2
! L0 t9 n0 @: R& ?3 {检错概率的数学模型
4 v  S  D+ V" e  t% @9 TCRC的检错概率可以近似通过以下公式进行估算：

vkrxvwac1xd64044431619.jpg

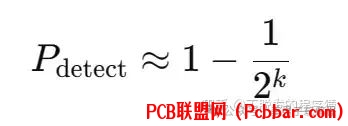
2 Y8 y* a6 o6 Y+ N$ R# Y) r其中 k为CRC校验码的位数。
. m5 Z; a) x4 j/ F6 J1 R& F
例如，对于一个8位的CRC码，理论上可检测到的错误概率约为 1?1/256=0.996。从公式中可以看出，位数越多，检错概率越高。
+ p" k: o  R. U3 K) @: S, ]3
根据信息长度 n 和所需检错概率 p 计算CRC位数
在实际应用中，我们可以通过以下步骤来确定CRC的位数：确定目标检错概率：假设我们要求的检错概率 Pdetect≥p。

# p$ B" z* R/ z代入公式并求出位数：我们可以重新排列公式来得到最小的CRC位数：
! S9 Q' o9 `2 O. B

5hnnjxxd4il64044431719.jpg

例如，若我们希望检错概率 p=0.999，则：

33vw2bzldje64044431819.jpg

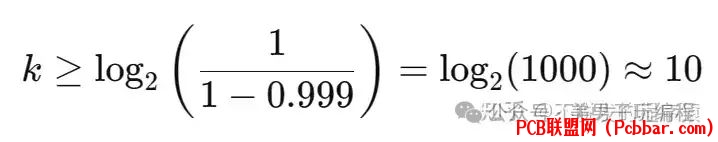
  K+ I6 U, ~' E这意味着至少需要10位的CRC才能满足这个检错概率。

考虑信息长度 n：虽然理论上，CRC的检错能力与信息长度 n 不直接相关，但在极长的帧中，可能会遇到极端情况。

因此，当 n 非常大（如数百甚至上千位）时，建议增加1-2位以提高稳健性。
: e( ?$ Z& d/ h( B5 b5 ?. s+ r4
CRC位数选择的经验法则
& o: {" `) |  u; z# n# Q

短数据帧（如10-100比特）：通常8位的CRC码已经可以提供很高的检错概率，适合普通通信应用。

中等数据帧（100-1000比特）：16位的CRC是更合适的选择，适合要求较高检错概率的协议。

长数据帧（1000比特以上）：32位CRC可以提供极高的检错能力，多用于高可靠性的工业、通信或存储系统中。

假设你设计的协议需要保证检错概率不低于 p=0.999，且每帧数据为 n=500 比特。
& r. L& u1 R, P( m/ |" k! c
9 S" g5 X. A/ k) E  D/ K, c) s根据上面的公式，我们计算得到的最小位数约为10位；结合数据帧长度，实际应用中推荐至少选择12位甚至16位的CRC，以确保满足高检错需求。

) x/ M1 A4 U5 \$ ]2 H$ m进一步的，标准CRC多项式（如CRC-16或CRC-32）经过广泛验证，在通信和存储应用中可靠性高，通常推荐直接采用这些标准多项式。
4 x) c+ [3 s9 F, G. Z5
CRC码位数对系统的影响
位数越长的CRC校验码，校验性能越好，但代价是数据包的开销和计算复杂性增大。
) f% t' l' {* K4 x8 L! B; Q9 ^
典型的实现中：
) z' j" Z5 I0 D* R5 f2 v

计算性能：硬件CRC加速器可以显著降低较长CRC的计算延迟。

通信开销：8位CRC增加的传输开销通常较小，但超过16位时，额外开销对低速通信协议影响较大。

  T- D! O5 a7 g  o( \' {综合以上分析，为了在实际应用中确定CRC码长度，建议的步骤如下：
% f* }7 J3 f  Z% @/ t1 P" n

根据要求的检错概率计算最小位数。

考虑数据帧长度，适当增加1-2位以提高稳健性。

使用标准CRC多项式以确保通用性和可靠性。
; r& R! H+ w- t" y9 Z8 `, P1 v4 m
; m. C5 @$ O$ z  g; E% A# E

pa2u5r01uci64044431919.jpg

- }3 p: F# x5 w# c

d0vuz2dwazn64044432019.gif

+ d' I1 }, a6 |- g点击阅读原文，更精彩~