浮点数精度问题全解析

嵌入式大杂烩

0、导读这篇文章主要探讨了浮点数在计算机中的表示、存储和精度问题。通过详细的解释和示例，您将了解浮点数误差的根源。文章内容较多，大约3700余字，阅读时间约为10分钟，建议先收藏，待有空时再细细品读。
1、引言0.1 + 0.2 为什么不等于 0.3 ？
当被问及浮点数为何存在误差时，你将如何回答？
没看完这篇文章之前你可能会回答:"哼，反正我就知道有误差..."
阅读完这篇文章后，你将能够更准确地回答这类问题，让我们开始这段学习之旅吧！
2、浮点数存储格式浮点型在内存中的存储不是像整形那样直接存储的，而是用一种二进制的科学计数法来表示的,具体的数学表达式为
V = (-1) s × M × 2 e其中，e = E - 127
在计算机科学领域，IEEE 754 是一种标准，用于定义浮点数的表示方法，浮点型数据的存储格式如下

2kxhas1phfb640971416.png

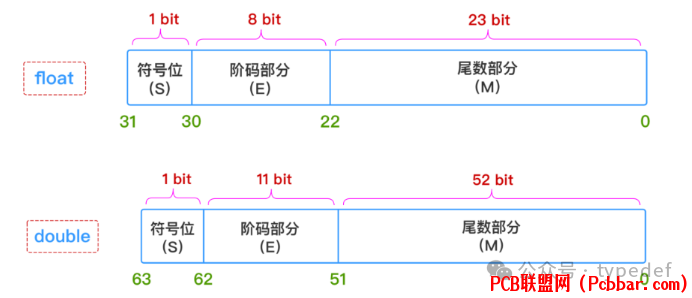
请务必记住，尾数存储用原码，阶码存储用移码

S(符号位)：0代表正数，1代表负数。

E(阶码)：指数字段需要同时表示正指数和负指数。为了得到存储的指数，在实际指数上加一个偏置，其中e=E-127。

M(尾数)：一个规范化尾数就是小数点左边只有一个1，然后是小数点后面的尾数部分。注意本文后续使用的e表示科学计数法中的指数部分，E表示存储格式中的阶码，默认的对象都指单精度的浮点数。
3、转换流程接下来我选择了一个恋爱脑的数字，将1314.520转换到32位单精度IEEE 754二进制浮点表示标准。
3.1、将整数部分转换为二进制将整数部分反复除以2，并记录每次的余数，直到商为0为止。
division = quotient + remainder;
1314 ÷ 2 = 657 + 0;
657  ÷ 2 = 328 + 1;
328  ÷ 2 = 164 + 0;
164  ÷ 2 = 82  + 0;
82   ÷ 2 = 41  + 0;
41   ÷ 2 = 20  + 1;
20   ÷ 2 = 10  + 0;
10   ÷ 2 = 5   + 0;
5    ÷ 2 = 2   + 1;
2    ÷ 2 = 1   + 0;
1    ÷ 2 = 0   + 1;
从上面构造的列表的底部开始取所有余数，即为整数部分的二进制表示。131410=101 0010 00102
3.2、将小数部分转为二进制将小数部分不断乘以2，并记录每次的整数部分，直到小数部分为0或达到所需的精度为止
#) multiplying = integer + fractional part;
1) 0.52 × 2 = 1 + 0.04;
2) 0.04 × 2 = 0 + 0.08;
3) 0.08 × 2 = 0 + 0.16;
4) 0.16 × 2 = 0 + 0.32;
5) 0.32 × 2 = 0 + 0.64;
6) 0.64 × 2 = 1 + 0.28;
7) 0.28 × 2 = 0 + 0.56;
8) 0.56 × 2 = 1 + 0.12;
9) 0.12 × 2 = 0 + 0.24;
10) 0.24 × 2 = 0 + 0.48;
11) 0.48 × 2 = 0 + 0.96;
12) 0.96 × 2 = 1 + 0.92;
13) 0.92 × 2 = 1 + 0.84;
14) 0.84 × 2 = 1 + 0.68;
15) 0.68 × 2 = 1 + 0.36;
16) 0.36 × 2 = 0 + 0.72;
17) 0.72 × 2 = 1 + 0.44;
18) 0.44 × 2 = 0 + 0.88;
19) 0.88 × 2 = 1 + 0.76;
20) 0.76 × 2 = 1 + 0.52;
21) 0.52 × 2 = 1 + 0.04;
22) 0.04 × 2 = 0 + 0.08;
23) 0.08 × 2 = 0 + 0.16;
24) 0.16 × 2 = 0 + 0.32;
虽然我们没有得到任何等于0的小数部分，但是我们有足够的迭代(超过尾数限制)。
从顶部开始依次取乘法运算的所有整数部分，即为小数部分的二进制：0.5210=0.1000 0101 0001 1110 1011 10002
3.3、规范化前面得出了整数以及小数部分的二进制表示，合并以后即：
1314.5210= 101 0010 0010.1000 0101 0001 1110 1011 10002
将小数点向左移动 10 位，使其左边只剩下一位非零的数字
1314.5210= 101 0010 0010.1000 0101 0001 1110 1011 10002= 101 0010 0010.1000 0101 0001 1110 1011 10002 ×2 0= 1.0100 1000 1010 0001 0100 0111 1010 1110 002 ×2 10
再回顾一下浮点数的数学表达式 V = (-1) s × M × 2 e 由此可知
s = 0
M = 1.0100 1000 1010 0001 0100 0111 1010 1110 00
e = 10
3.4、调整阶码根据规范化得知指数 e = 10，又根据公式 e = E - 127 可得知道 E=137，所以八位阶码的二进制表示如下所示：
E = 13710 = 1000 10012
3.5、尾数舍入由第三步规范化得出的尾数M有34位，但是存储格式中尾数只有23位，下面划线的是多出的部分，所以需要对尾数按照一定的方式进行四舍五入。
M = 1. 0100 1000 1010 0001 0100 011 1 1010 1110 00
一共有四种舍入方式，

向偶数舍入，就近舍入(默认)。

朝0舍入：即朝数轴零点方向舍入，即直接截尾。

朝正无穷舍入：对正数而言，只要多余位不全为0则向最低有效位进1；负数则直接截尾。

朝负无穷舍入：对负数而言，向最低有效位进1；正数若多余位不全部为0则简单截尾。向偶数舍入，简单理解就要让尾数的最后一位为0，让其保持偶数，能够被2整除。当尾数的最低位为0时，已经是属于偶数了，无需处理。当尾数最低位为1时，需要加1，使其保持偶数。
因为本例计算出尾数的最后一位为1，按照就近舍入(向偶舍入)原则需要加1使其保持偶数。
所以经过调整后的M为
M = 0100 1000 1010 0001 0100 011 + 1
M = 0100 1000 1010 0001 0100 100
3.6、组三元素根据前面的步骤可以得知
s = 0
E = 1000 1001 2
M = 0100 1000 1010 0001 0100 100 2
1324.5210 = 0-1000 1001-0100 1000 1010 0001 0100 1002
我们去一个转换网站上验证一下转换结果，网站链接放在文章末尾了。

qbpigsntumj640971516.png

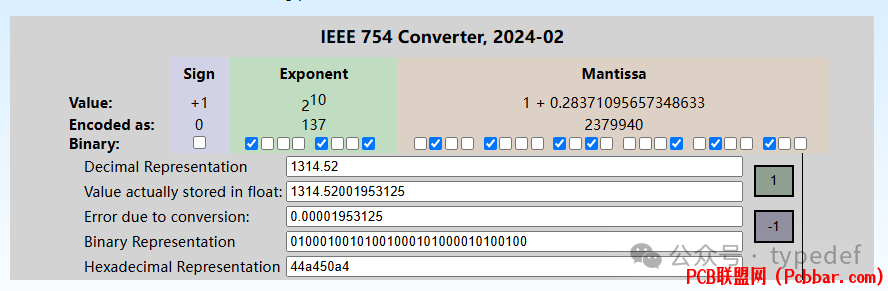
floatConverterIEEE754可以看到，跟我们转换的结果是相同的，说明网站转换也是选择向偶数舍入的。
4、单/双精度浮点数比较4.1、存储格式类型符号位指数长度(Bit)尾数长度(Bit)float1823double111524.2、精度浮点数的精度是由尾数的位数来决定的。
对于float型浮点数，尾数部分23位，换算成十进制就是 2^23=8388608，所以十进制精度只有6 ~ 7位；
这里的数字6和7可能会引起疑问，如何理解它们呢？
由于浮点数尾数的舍入问题，最后一位可能存在舍入误差，因此不完全准确。因此，可以准确表示的是后六位，而第七位则可能含有误差。
对于double型浮点数，尾数部分52位，换算成十进制就是 2^52 = 4503599627370496，所以十进制精度只有15 ~ 16位
类型有效位字节数float6 - 74double15 - 1684.3、浮点数范围类型最小值最大值float1.175494351 E - 383.402823466 E + 38double2.2250738585072014 E - 3081.7976931348623158 E + 3084.4、浮点数比较浮点数的比较通常用两数之差的绝对值小于一个自定义的数值时，代表两者相等，如下所示:
/**
*Author:(公众号:typedef)
*/
#define FLOAT_EPSILON (0.000001) //Define your own tolerance
#define FloatIsEqual(a, b) ((fabs((a)-(b)))
另外一种方法是将浮点数同时放大一个倍数，然后转成整数之间的比较，比如同时放大10000倍等。
5、阶码相关问题探索首先阶码E是用移码表示的，那么问题来了，什么叫移码？移码怎么计算？移码的含义是？浮点数为什么要用移码表示？
在解答这些知识点时，我们需要下面两点需要达成一致

阶码使用的是非标准移码

阶码是一个无符号的整数5.1、什么是移码移码是补码表示中最高符号位取反的结果。举个例子，上面计算1314.52时，指数是为10的。
+1010 = 0000 10102（真值）
原码：0000 1010
反码：0000 1010
补码：0000 1010
移码：1000 1010
所以10对应标准的移码 1000 1010 。
5.2、如何计算移码注意浮点数中移码的计算是非标准的，仅偏移2n-1-1=127。所以移码的计算公式如下所示，其中n为阶码的位数：
E = e + 2 n-1 - 1
E = e + 127
所以10对应的移码为137。
5.3、为什么要用移码表示它通过将数值加上一个固定的偏移量，使得原本可能是负数的数值变为非负数，从而简化了计算机中有符号数的表示和比较操作。使得计算机能够直接使用整数运算来比较浮点数的大小。
6、指数e6.1、指数范围浮点数指数部分的实际取值范围是 [-2(e-1)+2, 2(e-1)-1]，其中 e 为指数所占位数。32位浮点数，指数占8位，实际取值范围是 [-126, 127]。
-127用作表示0，128 用作表示无穷大和 NaN。NaN 是 "Not a Number" 的缩写，中文意思是“非数字”，通常用于表示一个未定义或不可表示的值。
换言之，8位阶码的表示范围是[0, 255]，其中0和255用于表示特殊值。因此，根据公式推导，指数e的实际取值范围是[-126, 127]。
6.2、特殊值形式指数(e)阶码(E)小数部分零-12700无穷1282e-1 = 2550NaN(非数)1282e-1 = 255非07、文中问题解答此时再来回答文中引言提出的问题， 0.1 + 0.2 为什么不等于 0.3 ？
/**
* Author:(公众号:typedef)
*/
#include
int main() {
  double a = 0.1 + 0.2;
  printf("%.17f", a);
}
输出为0.30000000000000004，由于在尾数舍入时会带来一定的误差，所以并不完全相等。
当在被问及浮点数为何存在误差时，你将如何回答？欢迎文章留言说出你的看法。
如果不从技术的角度回答这个问题，可以这样回答：整数是离散的，有限的并能够被计算机表示的，小数部分是连续的，包含无穷多的数，数量之多是无法被计算机存储的，只能存储计算机能够表示的最接近这个数值的小数部分，所以可能会不相等。
8、参考链接

https://www.cnblogs.com/gyunf/p/12816817.html

https://www.h-schmidt.net/FloatConverter/IEEE754.html

https://zh.wikipedia.org/wiki/IEEE_754

https://docs.pingcode.com/ask/304021.html9、总结本篇文章深入分析了浮点数的存储格式到转换流程，再到指数e以及阶码E的探索，大家应该对浮点数有了更全面的理解。
猜你喜欢：
一个非常轻量的嵌入式日志库！
一个非常轻量的嵌入式线程池库！
Github上热门 C 语言项目汇总！
实用 | 10分钟教你通过网页点灯
WiFi6+蓝牙+星闪，三合一开发板，真香！