电路拓扑的问题分析（1）--互连和双绞线的模型分析

电子设计联盟

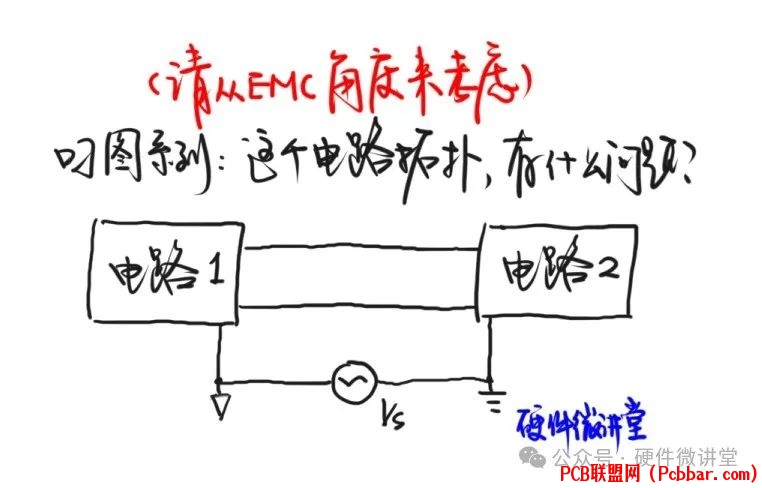
前段时间发了一个问题，即下图，问这个拓扑有什么问题？
! ~" q  R/ T+ `: V

kdu1taunm5b64013535005.jpg

. L# T" h# L0 X' p: ~  [* U
; }* i6 V% v& ^3 }! j
+ U' i+ K. P& V. Z0 m. J1 x
; N$ V* @5 E7 p! m到底有什么问题？

这个电路拓扑存在几个问题，我们先来看最直观的一个问题。如下图所示，电路1和电路2之间互联，这种互联可以是电源的互联，也可以是信号的互联。但无论是电源还是信号，都必然有去有回，需要回流。

43u5c3zdtjg64013535205.png

如上图所示，红线和蓝线之间间距较大，则存在较大的回流环路。这里无形中形成了一个很大的环形天线，可以接收外部空间的噪声能量，进而对内部电路产生影响。
环路多大，才算大？环路多小，才算小？不清楚的同学，可以看看前面的技术文章《电路的环路怎样才算小？?如何定量判断？》

/ M4 q& A" ~6 u0 N, K9 ?& `- v1 v7 `+ l
9 @0 N' r7 f2 D- }
, ?3 L9 ?' C4 c7 l7 t怎么办？
7 K% ^! Z  C. Y5 y+ C$ N: V- b3 r" A
针对上面提到的环路问题，怎么办呢？
两个电路之间的互联，采用紧耦合的方式，尽可能减小回流环路。可以使用屏蔽同轴线、双绞线；如果有多个信号，可以考虑使用带有参考层的FPC线（注意不是FFC线）等等。
& ?/ j' z( }, b% U" G& v" h顺带提一下，这里提到的双绞线是一种性价比很高的互联方式。它对电场耦合和磁场耦合都有较好的防护效果。
7 c( W, [7 C$ A1 }  M8 ^! {
为什么双绞线可以对电场耦合和磁场耦合有较好的防护效果？
% K5 K: v+ W4 p* T4 a3 o6 _如果要定量分析这个问题，并不太容易。我们逐步分解，线说下电场耦合。

+ z" b& x9 r+ d- Y
两根导线间的电容耦合

6 w% P9 i0 L0 P- Y# \4 h针对线束而言的电场耦合，其实是一种容性耦合。简单来说，就是一个信号线对另一对双绞线进行攻击，攻击的物理介质就是两者之间的寄生电容。但是一开始直接讲一根线攻击一对双绞线，涉及3个分析对象，模型有些复杂，我们先聊一下一根线攻击另一根线的情况。

kbgm5yuc4u064013535305.png

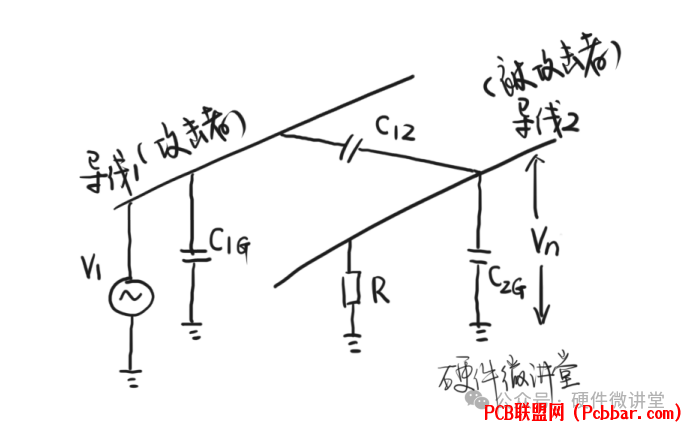
如上图所示，导线1是攻击者，导线2就是被攻击者，两者之间存在寄生电容C12。导线1对地存在寄生电容C1G，导线2对地存在寄生电容C2G。V1是导线1上的信号源，R是导线2的负载，Vn就是导线2上所耦合到的噪声电压。我们就是要分析下Vn的定量关系。
我们对上述模型做进一步简化，如下图所示：

ykbryn5wipj64013535405.png

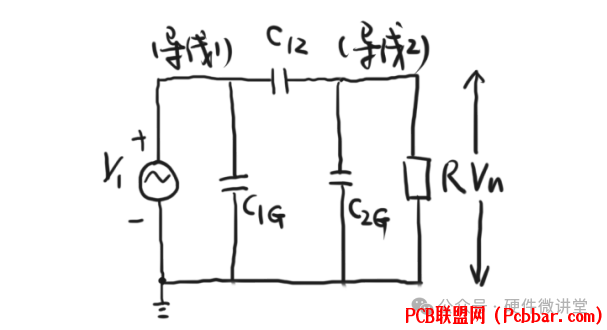
4 r, v& P+ N- O; T8 o  uV1、C1G、C12、C2G、R、Vn这些物理量，可以通过上述电路模型联系起来。这样，整个电路就是R和C2G并联后，和C12串联，之后再和C1G并联，Vn就是R||C2G两端的电压。于是就有下面的一些列计算：
2 H$ H! u- W" Z% M, [

xn2qn41bamu64013535506.png

6 M! g* m5 |6 N当然，上面得出的Vn关系式有些繁琐。我们加上一些前置条件，假如R很小，远小于……
5 a6 y. m4 F& ^6 j2 x

ctc2doqwbh064013535606.png

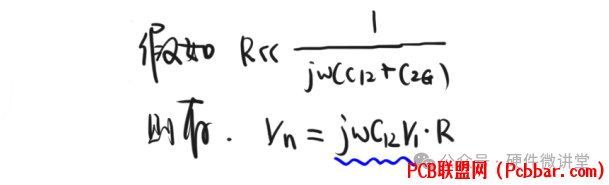
根据欧姆定律，Vn=jwC12V1*R，那么电流I=jwC12V1,相当于是由V1和C12构成的电流源。电路模型做进一步简化，如下图所示。
+ Y8 b" e0 z  a9 `# n) I

hop0rdq024464013535706.png

再假如R很大，远大于……

3 r# ]4 E/ t& b8 Q$ A$ P4 d

nwiik5wrz5p64013535806.png

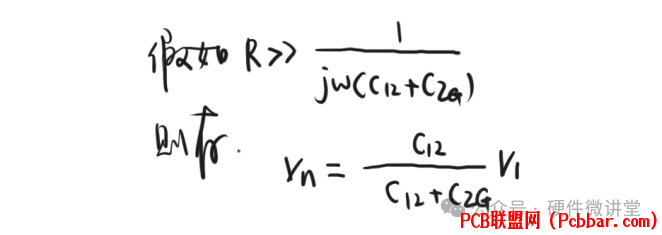
. U) k7 Z. J2 A( [根据串联分压原理，这里的Vn就是C12和C2G对V1分压后的电压。电路模型做进一步简化，如下图所示。

jb1y2vc24cu64013535906.png

8 r( p6 ]; Z9 Z( F( {# {/ F$ B. N% p. ?时间情况是在大多数情况下，导线2对地的阻抗不会很大，所以这种电容耦合可以简化为电流源。


% A$ ]. S9 I8 \/ s0 q' y
3根导线间的电容耦合

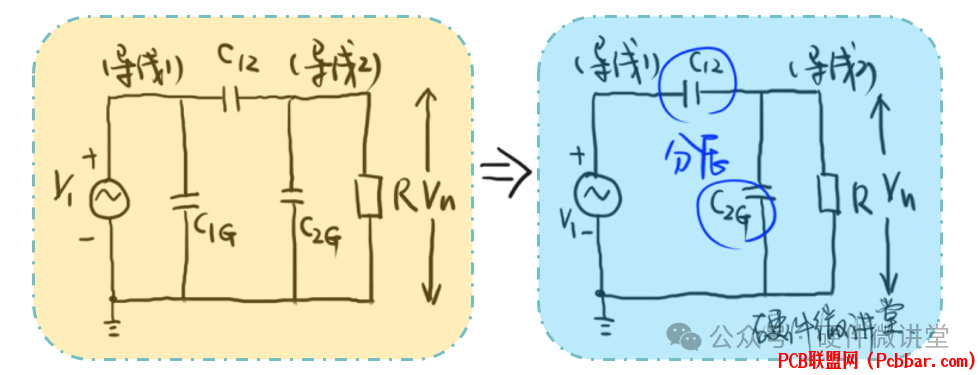
0 O) h6 k9 _* C上面我们讨论了2根导线之间的电容耦合。下面我们讨论下3根导线，一根是攻击者，另外两根是双绞线，作为被攻击者。根据前面讨论的内容，我们可以把耦合模型简化如下：

uedvbky2vfu64013536006.png

$ D' f- a0 w$ ~: w导线1上的V1在导线2上通过寄生电容C12容性耦合的噪声电压为Vn2，导线1上V1在导线3上通过寄生电容C13容性耦合的噪声电压为Vn3。则有：

42nckddi3mv64013536106.png

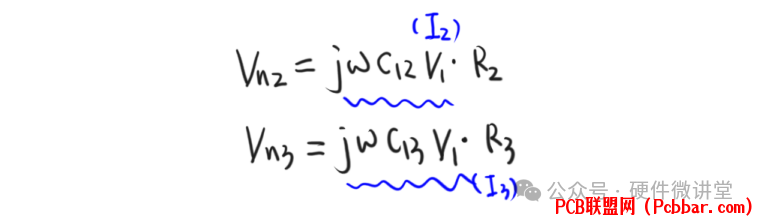
如前面所述，导线2和导线3是双绞线，两者是紧耦合的状态。那么，导线1和他们两者相邻，甚至缠绕在一起，距离基本相同，可以认为寄生电容C12和C13是相等的。
仅仅是这样，还不太够。如果双绞线终端上的负载R2和R3相差较大，那Vn2和Vn3也会有较大差异。

; `! p* T* l9 Y8 X2 l( G% w+ v
% s, s3 X! _- Q0 f) P" }& {: Q  M# ~平衡电路

# h. j/ ]8 }% e2 A  F: t基于前面所述，寄生电容C12=C13，如果R2和R3再相等，那么Vn2等于Vn3。在什么情况下，R2和R3相等呢？平衡电路，负载要平衡。度娘给出的解释如下。
0 x+ Q8 _, Z2 Y  c8 R  r3 T平衡电路是一个双导线电路。在平衡电路中，两导线和与之相连的所有电路的对地阻抗一级做所有其它导线的阻抗都是相等的。典型的平衡电路是差分放大器。
--百度百科
如下图所示，平衡电路Rs1=Rs2，In1=In2，R2=R3，如此可得出Vn2=Vn3。
% J& @7 A. n0 J* L

krf1hy4ngiu64013536206.png

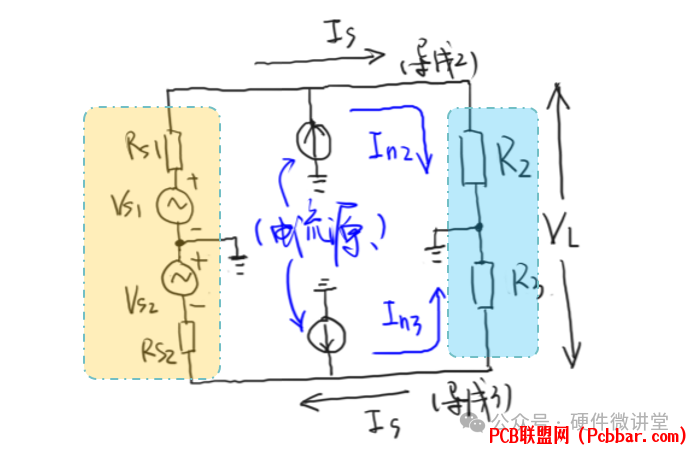
( m5 \5 A& P: I' L9 @/ d可是即便Vn2=Vn3，又怎样呢？
( g/ W( A3 d& a3 |我们进而可以推导出负载端的压降VL=Is(R2+R3)+Vn2-Vn3。由于Vn2和Vn3相等，电容耦合的噪声电压在负载处可以抵消，则有：VL=Is(R2+R3)
) W" v$ s* k- y* `: t

wlilfr2ifwm64013536306.png

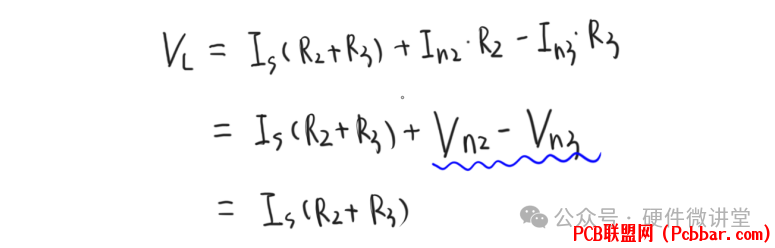
9 r1 d+ N4 O$ ]) m/ M% S由此也可以得出一个结论：双绞线防护电容耦合（电场耦合），需要有个前提是终端平衡。如果双绞线的终端端不平衡，即便感应电流In2=In3，但由于R2≠R3，电容耦合的噪声电压Vn2≠Vn3，噪声在负载端无法抵消。

# ]3 I+ m5 E5 z- O) g# K
, l+ g$ V, ?0 r( c9 u磁场耦合的防护
, h) C; Q. ~* f- N) A% N, U
上面是对双绞线对防护电场耦合的探讨。下面我们再探讨下双绞线对磁场耦合的影响。
" k5 F, x5 |3 _7 }导线1在有电流流过时会产生磁通，可以通过安培定律来确定磁通的方向。双绞线2和3沉浸在导线1的磁场中，磁力线会穿过双绞线绕城的环。如此一来，在双绞线的每个环中都会感应出感应电动势。

e1v4r1kdfv564013536406.png

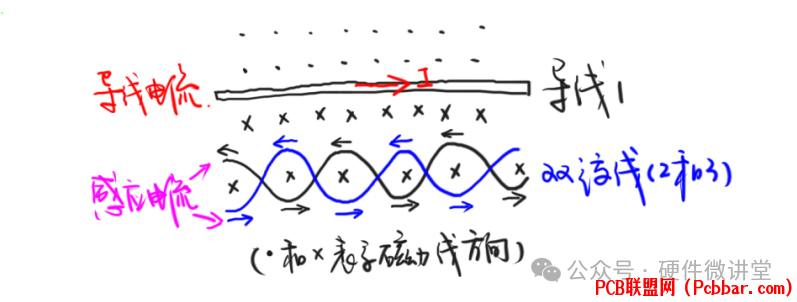
结合导线1的磁通方向及变化趋势，根据法拉第电磁感应定律，可以确定在双绞线的每一个小环中感应电流的方向，如上图中黑色和蓝色箭头。而在同一根到线上，可以看到相邻的两个小环上，电流大小相等，方向相反，感性电流相互抵消。如此，磁场耦合对双绞线中信号的干扰就被有效地减小了。
9 L2 w5 G7 E  o4 F: [" \6 w上面讨论的内容，需要用到楞次定律和右手螺旋法则。定律和法则的具体内容和分析过程这里不做赘述，网上这块的资料很多。
到此，我们已经把双绞线能够有效抑制容性耦合和感性耦合的原因、分析逻辑、推导过程、模型简化都做了解析，相信同学们应该会对双绞线有一个新的认识。

% ]9 S( U, Y: ?
6 }+ I9 V4 ?' _+ G2 z. U% n& \总  结

! s2 [. u4 h7 ^( X6 b今天要聊的，基本就这些。梳理下今天讨论的内容：
①感谢同学们在留言区高质量的回复；
②针对电路拓扑提出一个问题：电路互联的环路过大，需要紧耦合；
1 }6 \  G" P' N* S③指出双绞线可以有效抑制电场耦合和磁场耦合；
④对2导体和3导体的电容耦合进行模型简化、公式推动、定量分析；
⑤增加平衡电路的解析；
' C& o  B2 G' E6 r3 J. v8 J* L⑥对磁场耦合防护过程的解析。
) s8 Y! ?! h+ z+ F# Z本文的参考文献：
& z+ c1 s" s* s- j! F1、Paul《电磁兼容导论》；2、Ott 《电磁兼容工程》
3 P( R1 O3 V" A  `$ Z
怎么样？一个简短的问题，给出的回答可浅可深，就看你对这个知识点的理解达到怎样的程度。你学废了么？

- L, l8 X- S4 m0 k1 V/ A5 R
声明：
本文转载自硬件微讲堂公众号 ，如涉及作品内容、版权和其它问题，请联系工作人员微（13237418207），我们将在第一时间和您对接删除处理!投稿/招聘/广告/课程合作/资源置换 请加微信：13237418207
- b" l" n, J% D$ B4 d; p  N! ]& u
$ I( D. a, @8 k6 P, w                                                       
                                                               
                                                                       
0 Q3 Z6 q3 Y% e* a                                                                               
4 k5 X5 m9 D; }' {0 f3 z

dbhp4cfp1bl64013536506.jpg

0 H& E+ n, r% Z                                                                               
. V0 t( m! H% Y" Y+ ^                                                                                        【推荐资料】开关电源案例及学习资料包
+ ]$ b+ o8 {0 R  e# C; t. v                                                                               
                                                                       
                                                               
                                                       
! u' N9 ?) `( S" B                                               
2 B: m" ?% D& q3 |- F- e/ a
1 C4 r/ J, s3 U                                                       
: B& G5 D, c9 r) \! Y  F! W                                                               
! i+ Y# J; K' V) i                                                                       
                                                                               

wixcwqqtmzf64013536606.jpg

                                                                               
0 q$ j6 X9 q" E! l# S                                                                                        LC 谐振电路
                                                                               
                                                                       
                                                               
                                                       
" g) s8 T4 F4 K+ h9 v1 x# K$ e                                               

                                                       
+ K+ A# `, [& e- \" V                                                               
                                                                       
                                                                               
* A7 ~5 A( w2 I

equ5vt2hdlz64013536706.jpg

' O7 N, H& b% z! }                                                                               
                                                                                        带你简单认识理解开关电源AC-DC和DC-DC