今天这篇文章来聊聊惠斯通电桥。
$ W$ j3 F5 `+ Q" E7 Y% l4 \& r1 k( A4 K- [, {
1. 惠斯通电桥
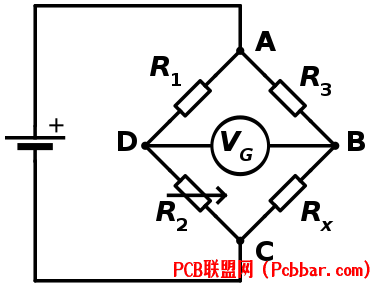
( w9 o$ ]# R: B惠斯通电桥(Wheatstone bridge)又称为惠斯登电桥,惠斯同电桥,是一种测量工具,用来精确测量电阻器的电阻值。电路的拓扑图如下所示:
; v9 z- ]- ~) d) k9 U* \+ R& _+ j4 A1 F9 |0 T% E, y
hu50v1g2qfz64018684557.png
$ f8 p6 {( ]1 p! q7 a1 }; Q
# G) q' r A5 ?电路拓扑工作原理如下:
$ X" E! M( v! {* t- y! s1)将精密电阻R1和可变电阻R2串联;+ p# i+ L! f P# H2 H
2)将精密电阻R3和待测电阻RX串联;
) D; H; P! V: E l/ x6 N4 ]3)在R1和R2的中点,R3和RX的中点接上检流计;
" O/ S; ~3 }, s4)当检流计的读数为0时,电桥平衡,便可以计算出RX的电阻值;
% Z& _- x- A( U: g上面即是惠斯通电桥的工作原理。从惠斯通电桥的工作原理可以看出,电路的核心思想是用四个电阻来测一个电阻的值。为了更加方便测量电阻,一般会将电阻的变化量转化为电压的变化,这样也便于后端的信号处理。' [* I( N$ ~$ O- r
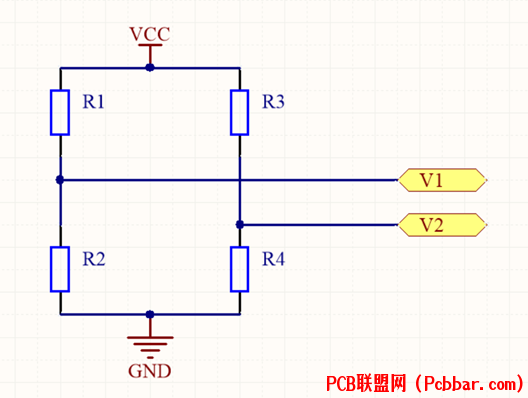
电阻和电压进行转换时,可以用下面的示意图。9 J( ]' F0 z2 t( |5 F
( f1 a; D/ Q% c3 F; d
2sgayvr1la564018684657.png
. w3 t+ _7 ^$ c. a1 {* b+ S/ ^# U2 L2 H- M% k1 u
, Z! E& G8 U) e1 {* C2 J6 \# E
rpzh4lidfha64018684757.png
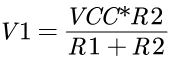
1 D7 h, L+ {; @, y6 O9 t" _/ n( \/ r
jvzjbhuaxd064018684858.png
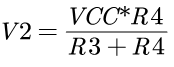 ) ]7 p' n c5 O. P; ~) ^1 f
) ]7 p' n c5 O. P; ~) ^1 f
# x h* C% v% g4 r3 i
当两桥处于平衡状态时,V1-V2=0。若有一个电阻发生变化,则V1和V2之间的平衡被破坏,输出电压将不为0。
6 J% {8 Z" b1 {) M有了上面这样的想法以后,惠斯通电桥可以理解为通过测量电压的大小来表征所测电阻的阻值。如果这个电路仅仅是做这种用途,那就太浪费它的功能,现在比较广泛的应用是基于惠斯通电桥的传感器。
5 W8 U) |: m8 F; ?惠斯通电桥传感器会将外界的物理量转化为成电阻的变化,而测量电阻直接使用电信号就能表示,因此外界的物理量比如压力的大小,形变的程度,扭矩的大小就和电信号对应起来了。
- X, a' u% p$ I下面这些场景就能看到惠斯通电桥的身影。
% K- m5 C" P- ?. ?- H% \2 e电子称
$ x/ a& n* w6 p0 G* w1 X6 ~7 h
20g34aoyijd64018684958.png

8 ]4 y" D, l2 _, d" G _) s
5 E' _$ h/ F- p* k车辆称重管理
6 `& E( ?9 Z/ v4 X
e3521wo3c4t64018685058.png
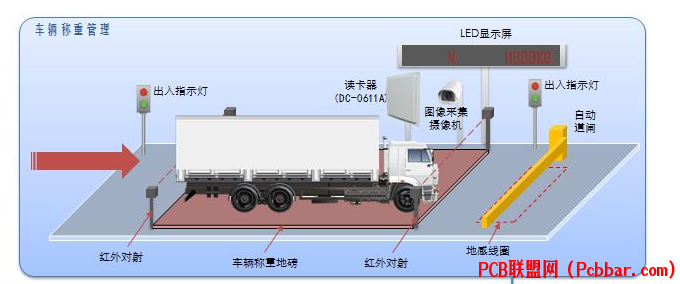
+ r4 Q4 n+ a, o9 \3 F2 P! ^0 _- i# @4 C, j, P
2.惠斯通电桥的分类
/ ]: N5 e9 z9 v1 a根据前面的介绍,惠斯通电桥有4个电阻,且其中一个电阻未知并且电阻的变化和外界物理量的变化有关。在设计原理上,根据电阻变化的数量,又将惠斯通电桥分为单臂式,双臂式和全桥式。下面将分别推导三种电桥的数学关系式。
3 n! M0 B/ s, v1 e" o2.1 单臂式$ X9 @$ s9 u. G& H9 Z
单臂式惠斯通电桥意味着只有一个电阻发生变化,如下图中的R1,而其他三个电阻保持不变。如下所示。
1 X) U% }# I. I( ]3 [$ B) I6 p" ?2 V
nbtu5dpn05464018685158.png
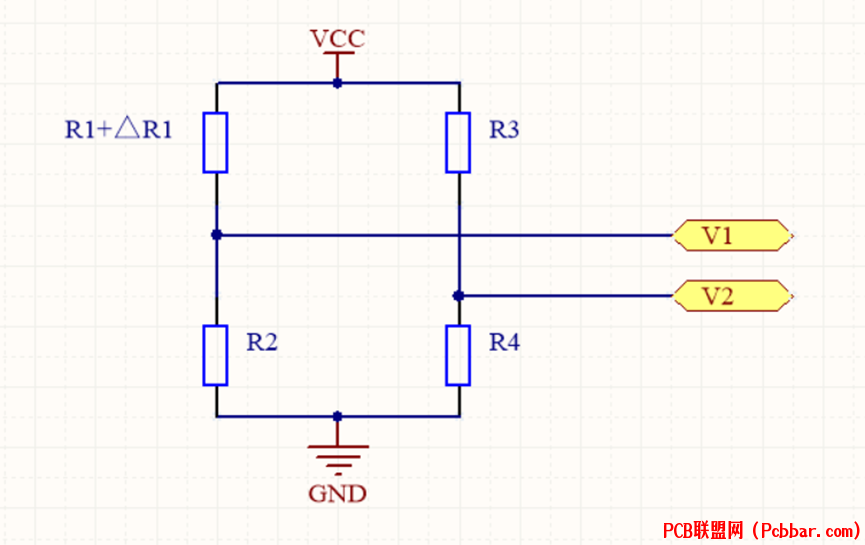 0 K) A4 @; ^# Q" n
0 K) A4 @; ^# Q" n
( e [7 @! A: m% q' R6 j' m
o12ofqzfpy164018685258.png
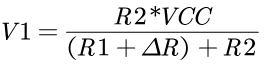
& b8 x3 R1 O9 H& x: E, a* U- p( s: w
同理可求V2,且上述电桥还满足R1=R2,R3=R4必须成立。
. {% w( R7 t; o" T$ |$ ~: `" O
mg2ygcpi5vd64018685358.png
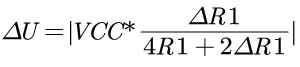
' _6 Q- F( l9 g7 K9 b; K) M; a& f/ T$ R
如果在设计时有
# @% J8 } R) }6 y% ~) u+ O2 I
+ A$ e7 M1 a1 A# W7 Y4 x0 F
hyze5q3qy3u64018685458.png
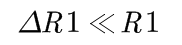 : b9 D7 @5 H, p. M: N' f
: b9 D7 @5 H, p. M: N' f
( N6 S1 L1 p& ]) J( v' ^
则输出电压的关系式可以化简为:
# Q& t& a6 J7 L2 K# q/ A' l% W" M0 F6 T$ N' I
21ovtsxlwo464018685558.png
 . h. W$ M7 h6 I5 \
. h. W$ M7 h6 I5 \
4 B+ ~/ p; Y Y1 O1 T+ \即输出电压大小和电源电压以及电阻R1的变化量有关。设计电路时使用确定的VCC给系统供电,那么输出电压只与电阻R1和其变化量有关。! u: N: Q5 p* n" ?7 f
1 f) y3 Y5 f4 y2.2 双臂式1 S" h( x& _8 R# s3 C$ v" N1 i, h8 t" L
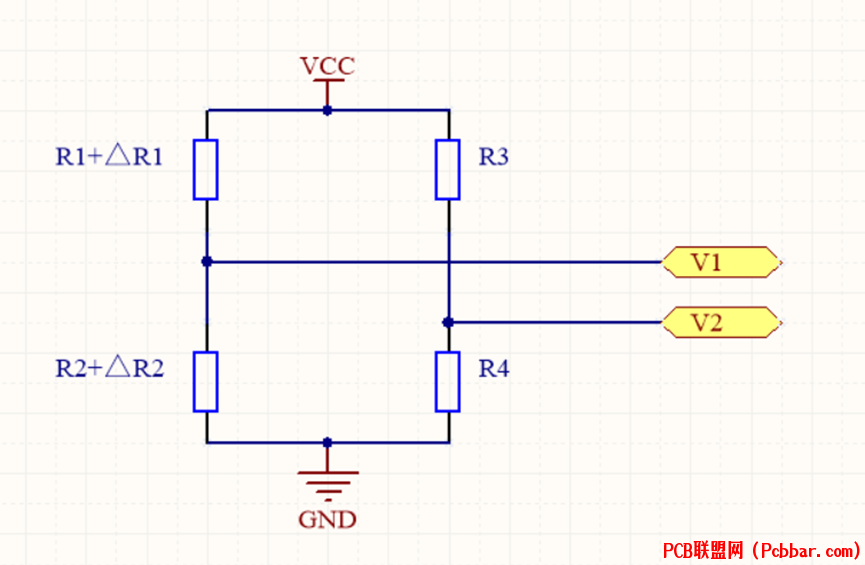
双桥臂意味着有两个电阻发生变化,类似于半桥。
, R% f. h U' p7 ` s6 x9 D8 `2 }% I2 t
w2rc0gfvyzw64018685658.png
 0 l$ k4 W6 j0 s4 g
0 l$ k4 W6 j0 s4 g
. w; Y9 A* E2 d: i( q
双桥臂的电阻和单臂式的电阻一样,必须满足R1=R2,R3=R4,且在变化的两个电阻R1和R2中,还需要满足它们的变化量呈现负相关。即满足:
" E' n+ X3 J( ?& A
js5hknpv3h164018685758.png
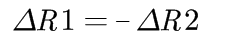 7 t t$ O) ~7 G
7 t t$ O) ~7 G
结合单臂式的推导公式 ,可以计算出双臂式的数学表达式如下:
2 |" e7 n& A8 a+ [1 }
ya1m3yb0q3a64018685858.png

7 o3 d& @8 k& n8 W+ a9 D p
# p; O; v* p! x3 s+ v' F双桥臂的输出电压也和电源VCC以及电阻R1本身及变化量有关。双臂式和单臂式相比,电压变化相差2倍,则可以判断出双臂式的电桥要比单臂式的灵敏度更高。; o; m$ t0 K* e3 U; R5 B
+ J! j; H2 w" m- O2.3 全臂式1 `9 c% r# O& l7 O% b( w n! T2 \
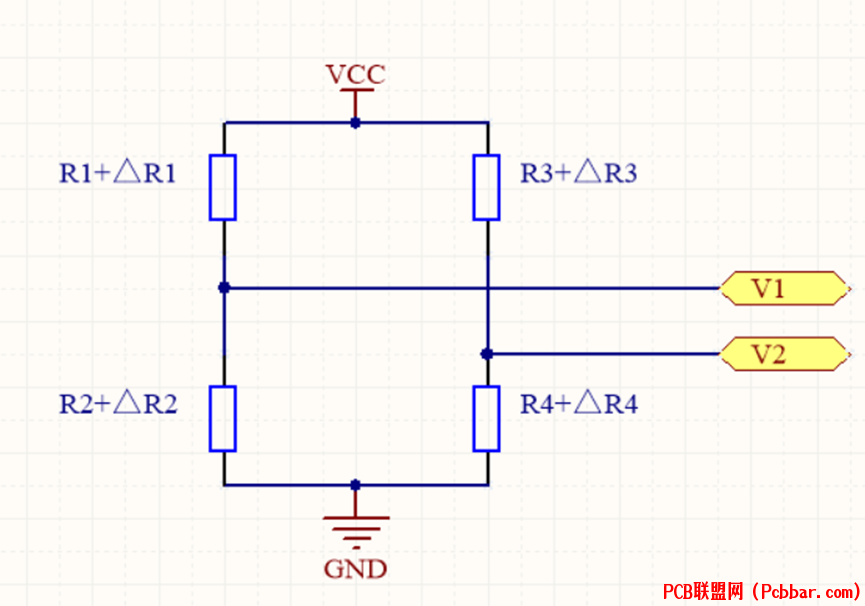
全桥意味着惠斯通电桥中的四个电阻都要发生变化,且电阻之间的存在的关系如下图所示。
+ J( g4 m& O0 r; L7 S9 H5 f2 S8 M# H1 r0 j2 ~+ f+ j2 d3 G2 `/ L; \
i3dtquoenwn64018685958.png
# w9 K0 l; P! A7 G) x! w2 z& k7 T: K# w) s$ o$ i4 m6 Q
4 S" B: J1 t Q在全桥臂中,电阻需要满足的关系如下:R1=R2=R3=R4,且( @8 {5 W# S( D& l" p% ]& w+ V' K
adz02ftysia64018686058.png
 7 e" a& m/ I% z7 y
7 e" a& m/ I% z7 y
相比单臂式和双臂式而言,对电阻的变化的要求更高。
( f0 _4 O* l( k( h! {& M' c- ~同理可以推出数学关系式为:' q- m& L" |( u& g1 X* F- `3 X
qkk2c31bsh064018686158.png
 3 [0 O: z+ o5 F/ C
3 [0 O: z+ o5 F/ C
全臂式相对双臂式电压相差2倍,和单臂式相差4倍,因此,灵敏度会更高。5 A8 G3 _0 \+ r8 e+ ?' j% A
/ C q/ K$ A$ b5 f& o4 K
3. 电桥灵敏度. I5 m, {2 ] c7 u) I
在惠斯通电桥中,对灵敏度的定义如下' A1 R3 p5 p7 v: H
if3ki1ckugr64018686258.png
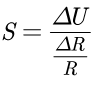 , `& X; a! g, y/ m# k0 Y' O! N
, `& X; a! g, y/ m# k0 Y' O! N
即单位电阻变化所产生电压的幅值。对同样的电阻变化,
" g N' M* u4 [9 H, p) a
iunqdw0mulq64018686358.png
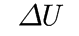 2 l5 R$ V3 e8 o1 g
2 l5 R$ V3 e8 o1 g
越大,灵敏度越高。所以如果追求高精度的测量,就要用全臂式的惠斯通电桥。
& i) A5 S# e! C. ?* m
' ~: v& t5 e+ A W; `4. 惠斯通电桥仿真0 [0 i5 d; T9 u
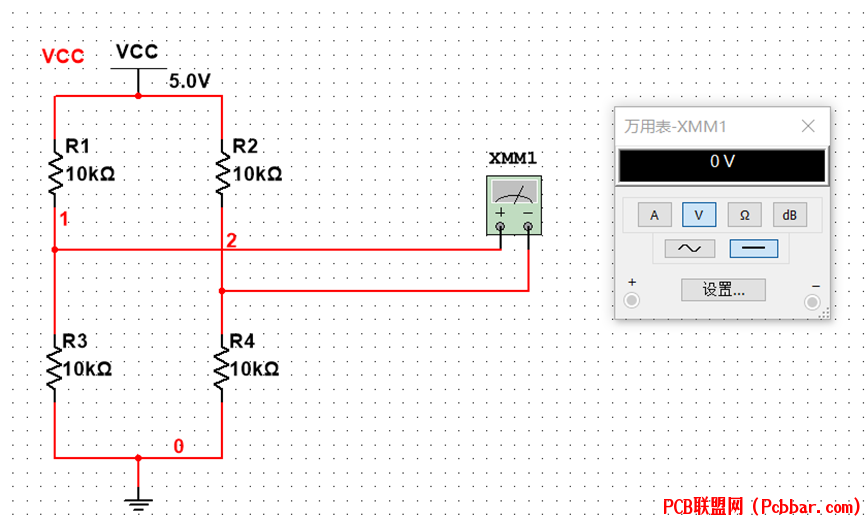
1)当电桥平衡时:
6 I ? O2 O% F5 Z) [根据电桥原理可知,平衡式的电压为0V,仿真一致。
: f. z$ z7 |: X) r
$ M v8 w- C& `5 I: Z% u
fi2wsi21wqf64018686458.png
5 X/ X4 k6 w8 M i
, I% t$ w& p4 D% S! r( F* d! G2)单桥臂电阻变化率为0.1
7 h( D/ N; `' g根据公式:: V3 X/ y5 x- T* S" C
- \0 U) X& y: Y2 h
计算电压为125mV,仿真119.046mV,其原因是在计算过程中变化量相对电阻自身来说,越小越好。此电路中仅仅只有0.1倍的差距。因此,仿真和计算存在5.954mV左右的误差。' _ r7 j. E( F9 P4 }$ I& @8 X
6 h# Y: h6 u. ^5 Z: W 3 Y% J9 ~2 Q2 l- {0 Z 3 Y% J9 ~2 Q2 l- {0 Z
3 a {5 C3 n/ N( T# W
3)双桥臂电阻变化率均变化0.1
0 k B& y8 t) O根据公式,
: e. {% x, {1 `( r- d: }$ M
5 h; f! a2 c. [6 p }; v) v) j( @计算值为250mV,仿真249.998mV,相差0.002mV
3 X8 K3 m: D5 Q, {! ~& \% l; s, u( V8 ]5 Q! Z
 & g" d7 S# E% h' E) Y & g" d7 S# E% h' E) Y
_6 m2 T) ^+ Z6 M
4)全桥臂电阻变化率均变化0.1* U6 I6 v5 [0 F( Z
根据公式
8 @ D b3 V( t4 r/ m2 }
# p" J! M5 z4 g4 W# x1 f- o( j1 S, {计算值为500mV,仿真499.995mV,相差0.005mV7 Q& [2 x$ k4 _& X# W
# I9 A( j) n' D5 I) P# ]: h# g
5 ] s7 J1 i3 N+ [' S2 @2 O% D' `" {: A, [9 }
从仿真可以看出,从单臂式到双臂式,误差从5.954mV降低到了0.002mV,但是从双臂式到全桥臂式,误差竟然增加了0.003mV,那设计全臂式不是没有优势吗?
T& r: P2 K6 t7 y) [5. 误差来源分析
2 [" B# l/ T# F }( G根据前面的公式推导,要满足计算关系式,需要满足的条件是
5 s6 T0 U) H- ^# ` 2 ?5 W9 t( g6 ~2 E1 m- U 2 ?5 W9 t( g6 ~2 E1 m- U
以单臂式为例,如果将电阻的变化率增加到0.001时,计算是1.25mV,仿真是1.248mV,误差0.002mV,此时单臂式的误差和双臂式达到同样的效果。# x& m0 {, U; O9 T
3 V8 o% H0 e [3 D5 b- |. ~: x
$ S; q! b+ |3 P" M4 l
3 l) b0 B" f4 J! Z1 I如果是双臂式结果会怎么样呢?8 a% f1 ~- B: V
仿真结果表示,此时双臂式和单臂式的效果一样,都是0.002mV的误差。) {( b! B0 l _" e
0 u3 E0 d: L6 k: A$ p! J
6 n8 o6 V* Z" l2 ]# s2 B! a9 }0 B5 h& [0 Z8 H! q
全臂式此时的误差还是0.005mV
" e4 ^/ }7 ~( j3 V1 k$ d- _: L3 W& m/ V# K9 d) K! w0 F9 G
! y, {7 F' z4 b& p, a v/ m
 : {! K) N% B* ~) t : {! K) N% B* ~) t
4 i- |# O- O/ W* O; d7 o( f( Y3 }上面的仿真和理论上有些区别,判断原因应该和仿真软件有关系。为了验证这个猜想,换用TI的TINA进行仿真
+ E# C3 Y: s' H3 p3 | d( c仿真后发现TINA的误差更大,直接以mV为单位,小数点后面都没有。用TINA软件仿真的误差更大。
8 b: s; q8 x' v% Z% Z. ~2 g) |7 l; o. g9 h) q

- Y' ~0 x* a/ {/ a" b
5 e6 y6 ^5 R: D: u. H那上面的问题怎么办呢?
_1 `" M4 \4 t0 N; M要解决这个问题,还要和后面的采样电路结合起来,0.005mV的误差到底会不会对后端的采样电路造成影响。 F6 M# K+ R# n" M7 \* k1 ?
假设后端用14bit的ADC进行采样,参考电压是2.5V,可以计算出1个LSB=152uV,避免采样中存在误差,要求最小偏差不能超过0.5LSB,即76uV,此时对于5uV的误差来说,完全可以忽略不计。因此,这个误差在实际项目中可以不用考虑。也许电源纹波带来的误差就不止5uV。
6 P2 t7 [! ]4 J8 @4 n) t( `" \: x8 H4 e. z
6. 总结
& u3 n- a+ i! m0 L1 t6 y- P3 h. o2 i本篇文章分享的内容主要介绍了惠斯通电桥的电路原理和三种应用广泛的拓扑。并且对电路进行实际的仿真。理论上全臂式的电桥灵敏度更好,但是仿真出来的误差,却比双臂式要大3uV,但是从实际使用来看,3uV并不会对电路造成影响。对此,你有什么看法?在实际项目中,你们更愿意选择哪种方案? |