无人机载合成孔径雷达系统研制手记（三）：结构设计与图像生成

美男子玩编程

“ 详细介绍了 SAR 无人机的结构设计及成像原理。 ”

xjxp5r43gru64092155.png

结构设计

kzvlek2azcx64092255.png

Blender中的无人机模型
无人机需要一些机械部件来将雷达固定在机身上。飞行控制器安装在机身内部，但内部没有足够空间容纳雷达，因此我设计了一个3D打印支架，将雷达PCB安装在无人机机身下方。这种安装位置还需要配备起落架，以防止无人机降落时直接压在雷达上。由于我不熟悉任何机械CAD软件，我使用Blender完成了这个设计。对于这些简单部件而言，Blender完全能够胜任。

riqpublhwgb64092356.png

无人机下方搭载雷达
雷达支架将雷达PCB固定在无人机机身上。为它配备某种防水防尘外壳会更好，但目前尚未完成。我在PCB上方覆盖了一些材料，以防起落架失效时保护电路板。
雷达支架通过四颗螺丝与无人机连接。无人机无线电控制器的天线可见于左下方。螺旋桨采用可折叠设计，这种设计显著提升了便携性，折叠后整机可装入背包携带。

xhbodysf42q64092456.png

接收器极化开关 PCB天线板通过两颗可调节角度的螺栓固定。飞行控制器的串口连接至其中一个JST接头上，另一个未使用的JST接头目前仅用胶带临时固定在原位。
发射端的极化切换开关和两个SMA接口集成在主电路板上，而接收端的极化切换开关因空间限制被单独放置于另一块电路板。虽然雷达支架上预留了安装孔，但由于SMA线材硬度较高，最终选择直接悬空固定该电路板。极化切换开关通过另一组JST连接器与雷达电路板相连。

gpp0w4uvtoe64092557.png

带起落架的无人机起落架采用直径10厘米的碳纤维管制作，末端配有3D打印的TPU材质端盖。虽然更小直径的管材可能也适用，但当前选用的碳管刚度极佳，在着陆过载时其他结构件会先于它们发生损坏。
雷达系统直接由无人机电池供电。通过XT60分线器将飞行控制器和雷达并联接入同一电池组。

4bwi3xsgp5s64092657.png

无人机在厨房天平上保持平衡无人机空载（不含电池）重量仅为752克（1.66磅）。配备两块六芯锂聚合物电池，其中容量较小的1300毫安时电池重196克，容量较大的2200毫安时电池重322克。使用小容量电池时，整套系统总重仅948克。雷达成像原理
雷达通过测量目标的距离与相位信息进行成像。为将这些测量值转换为雷达图像，可采用匹配滤波技术：针对图像中的每个像素点，生成该位置目标反射的参考信号；将测量信号与参考信号的复共轭逐次相乘，并对所有测量结果进行累加。当测量信号与参考信号高度匹配时，相位一致性会使乘积显著增强；若失配，则乘积表现为随机相位的复数，累加后相互抵消，最终呈现低响应值。
成像过程可表述为：

lerdz5ezzyo64092757.png

其中：

P 为图像像素集合

N 为雷达测量次数

Sn 为傅里叶变换后的测量中频信号sn

d(p,xn) 表示第n次测量时雷达位置xn到像素点p的距离

H?为图像中目标位置参考函数的复共轭（即该位置目标反射中频信号的傅里叶变换））
此方法称为反投影算法，其优势在于原理简单且无需对飞行几何路径进行近似假设，但计算量极大。例如，1 千米 x 1 千米的图像分辨率为 0.3 米，雷达扫描次数为 10,000 次，计算图像需要

0zo1agmfxh564092857.jpg

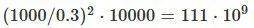
次反投影运算。这意味着一幅图像需要超过 1000 亿次的复指数和平方根计算，而图像大小和扫描次数在实际应用中可能更大。有一些巧妙的算法可以用来加快计算速度，但它们通常都是近似值，或者只适用于线性飞行轨迹。使用极坐标而非笛卡尔坐标是一种简便易行的改进方法，由于角度分辨率不变，图像中需要的像素较少，而在靠近雷达的地方，跨距分辨率较高。极坐标图像随后可插值到笛卡尔网格。

__global__ void backprojection_polar_2d_kernel(          const complex64_t* data, const float* pos, complex64_t* img,          int sweep_samples, int nsweeps, float ref_phase,          float delta_r, float r0, float dr, float theta0,          float dtheta, int Nr, int Ntheta, float d0) {    const int idx = blockIdx.x * blockDim.x + threadIdx.x;    const int idtheta = idx % Ntheta;    const int idr = idx / Ntheta;    if (idr >= Nr || idtheta >= Ntheta) {        return;    }    const float r = r0 + idr * dr;    const float theta = theta0 + idtheta * dtheta;    const float x = r * sqrtf(1.0f - theta*theta);    const float y = r * theta;    complex64_t pixel = {0.0f, 0.0f};    for(int i = 0; i         // Sweep reference position.        float pos_x = pos[idbatch * nsweeps * 3 + i * 3 + 0];        float pos_y = pos[idbatch * nsweeps * 3 + i * 3 + 1];        float pos_z = pos[idbatch * nsweeps * 3 + i * 3 + 2];        float px = (x - pos_x);        float py = (y - pos_y);        float pz2 = pos_z * pos_z;        // Calculate distance to the pixel.        float drx = 2.0f * sqrtf(px * px + py * py + pz2) - d0;        float sx = delta_r * d;        // Linear interpolation.        int id0 = sx;        int id1 = id0 + 1;        if (id0 0 || id1 >= sweep_samples) {            continue;        }        complex64_t s0 = data[i * sweep_samples + id0];        complex64_t s1 = data[i * sweep_samples + id1];        float interp_idx = sx - id0;        complex64_t s = (1.0f - interp_idx) * s0 + interp_idx * s1;        float ref_sin, ref_cos;        sincospif(ref_phase * d, &ref_sin, &ref_cos);        complex64_t ref = {ref_cos, ref_sin};        pixel += s * ref;    }    img[idr * Ntheta + idtheta] = pixel;}若在数年前，如此庞大的计算量堪称天方夜谭，但现代GPU技术已能在1秒内完成运算。该问题尤其适合GPU并行计算架构——每个像素的反投影运算均可独立并行执行。基于RTX 3090 Ti显卡的基础CUDA内核即可实现每秒2200亿次反投影运算（每次运算需执行平方根与复指数运算，后者可通过正弦/余弦函数实现）。考虑到当前实现仅为未经优化的直接算法版本，具备CUDA开发经验的工程师完全能通过优化手段进一步提升性能，且无需引入任何近似计算或精度损失。自动对焦

u4m0b2n0wtj64092957.png

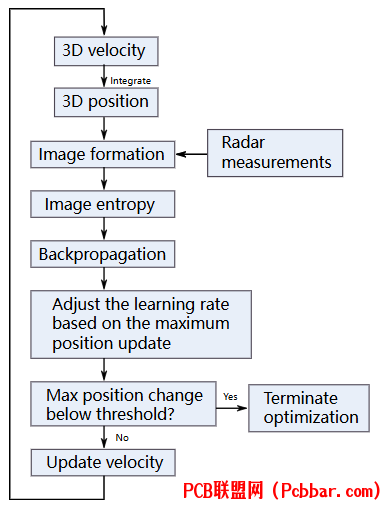
自动对焦框图
GPS 和 IMU 的定位精度不足以形成高质量的图像。理想情况下，位置误差应精确到波长的几分之一，但现有 GPS 的精度无法满足要求。为了获得高质量的图像，必须使用自动对焦算法，利用雷达数据信息对雷达图像进行对焦。
最常用的自动对焦算法是相位梯度自动对焦。这是一种简单、快速的自动对焦算法，其工作原理是将未对焦的雷达图像作为输入，求解出一个相位矢量，与图像的方位 FFT 相乘后得到一个对焦图像。但是，由于方位波束较宽，雷达基线较长，导致聚焦误差与空间有关，因此在这种情况下效果不佳。
我优化了之前的反向传播自动对焦，使用 PyTorch 并做了一些改进。这种自动对焦算法的工作原理是形成雷达图像，计算输入速度的梯度，并裁剪学习率，将最大位置变化限制在预定义值内。然后使用梯度下降优化器更新输入速度。我发现使用三维位置的效果并不好，因为它往往会将每个位置向随机方向推移。相反，使用速度并将其与位置进行整合，似乎会产生更好的效果。我们还加入了一个小的正则化约束，引入正则化项最小化优化位置与原始位置偏差，抑制过度修正。
根据最大位置变化调整学习率可以更容易地设置优化器元参数。我们不直接设置学习率，而是预设最大位置变化动态，并以此来设置学习率。
这是一种非常通用的自动对焦算法，对雷达系统、场景或飞行轨迹不做任何假设。其明显的缺点是，它需要多次形成雷达图像，使本已缓慢的图像形成速度更慢。如果没有 GPU 的快速图像形成，这种方法就会因为速度太慢而无法发挥作用。
自动对焦算法可在 Github 上获取：
https://github.com/Ttl/torchbp

原文转载自 https://hforsten.com/homemade-polarimetric-synthetic-aperture-radar-drone.html，已进行翻译及校对优化

注意：如果想第一时间收到 KiCad 内容推送，请点击下方的名片，按关注，再设为星标。
常用合集汇总：

和 Dr Peter 一起学 KiCad
KiCad 8 探秘合集
KiCad 使用经验分享KiCad 设计项目（Made with KiCad）常见问题与解决方法KiCad 开发笔记插件应用
发布记录